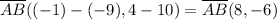 ;
; от точки A
от точки A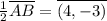 ;
; в обе возможные стороны
в обе возможные стороны перпендикулярен вектору основания
перпендикулярен вектору основания  , а значит его проекции накрест-пропорциональны с противоположным знаком:
, а значит его проекции накрест-пропорциональны с противоположным знаком: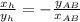 , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:
, что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:  (II) ;
(II) ; пропорционален вектору
пропорционален вектору  , поскольку для вектора
, поскольку для вектора  выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора
выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора  ;
; имеет длину
имеет длину 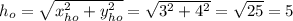 ;
;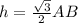 , т.к
, т.к 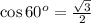 ;
;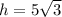 , а стало быть
, а стало быть  ;
;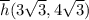 .
.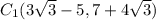 /// примечание:
/// примечание: 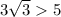 ;
;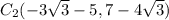 /// примечание:
/// примечание: 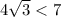 .
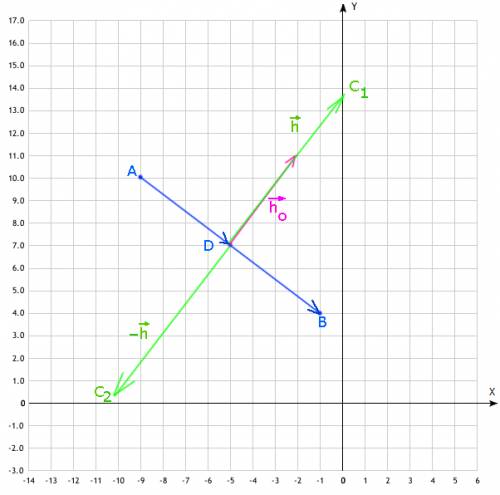
.
AB = AC =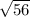 см
см
Объяснение:
Дано:
AC = AB, BC = 10 см, BM = 8 см, CM = MA
Знайти: AC,AB - ?
Розв'язання: Проведемо медіану до основи BC у точку K, тоді CK = BK =
= BC : 2 = 10 : 2 = 5 см.Нехай медіани AK і BM - перетинаються в
точці O.За теоремою про медіану, медіани точкою перетину діляться у відношенні 2 : 1, рахуючи від вершини кута.Введемо коефіціент пропорційності y, тоді BO = 2y,MO = y, так як медіани AK і BM - перетинаються в точці O.
BM = BO + MO;
8 = 2y + y;
8 = 3y;
y =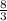 ;
;
BO = 2y = 2 *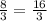 ; MO = y =
; MO = y = 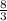 ;
;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора: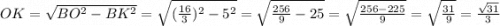 ;
;
Введемо коефіціент пропорційності x, тоді OK = x, AO = 2x за теоремою про медіану, так як медіани AK і BM - перетинаються в точці O.
AK = OK + AO;
AK = x + 2x = 3x = 3*OK =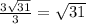 ;
;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора:
Так як AB = BC за умовою, то AB = AC =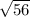 см.
см.