Через точку C, которая лежит вне параллельных плоскостей α и β, проведены прямые a и b, которые пересекают плоскость α в точках A и A1, а плоскость β — в точках B и B1 соответственно. Найдите AA1, если: AC = 2, AB = 6, BB1 = 10. С рисунком и подробно !
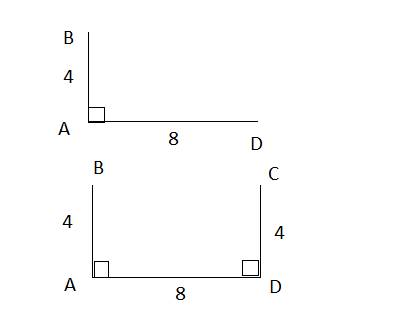

BD=CD по условию, а ED - общий катет. Отсюда ∠BDE=∠CDE,
а т.к. точки A,D,E лежат на одной прямой, то и ∠BDA=∠CDA.
(Заметим, что если Е совпала с D, то равенство углов ∠BDA и ∠CDA следует сразу из условия, т.к. BC⊥AD).
Далее, треугольники BDA и CDA равны по сторонам и углу между ними
(AD - общая, BD=CD по условию, ∠BDA=∠CDA доказали выше), а значит, AB=AC, что и требовалось.