Точка, лежащая на оси координат, имеет хотя бы одну нулевую координату. Расстояние между двумя точками определяется по формуле
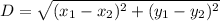
----------------------------------------------------------------
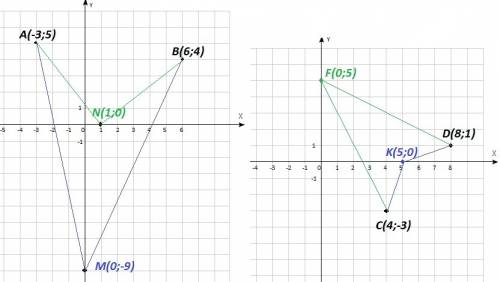
а) А (-3;5) и В (6;4) Нужно найти точку с координатами (x; y), равноудаленную от точек А и В
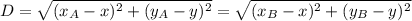
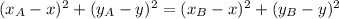
(-3 - x)² + (5 - y)² = (6 - x)² + (4 - y)²
9 + 6x + x² + 25 - 10y + y² = 36 - 12x + x² + 16 - 8y + y²
6x - 10y + 34 = -12x - 8y + 52
18x = 2y + 18; 9x = y + 9
x₁ = 0; 9·0 = y₁ + 9; ⇒ y₁ = -9
y₂ = 0; 9x₂ = 0 + 9; ⇒ x₂ = 1
ответ: две точки с координатами M(0; -9) и N(1; 0)
----------------------------------------------------------------
б) С (4;-3) и D (8;1) Нужно найти точку с координатами (x; y), равноудаленную от точек C и D
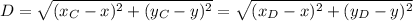
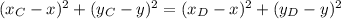
(4 - x)² + (-3 - y)² = (8 - x)² + (1 - y)²
16 - 8x + x² + 9 + 6y + y² = 64 - 16x + x² + 1 - 2y + y²
-8x + 6y + 25 = -16x - 2y + 65
8x = -8y + 40; x = -y + 5
x₁ = 0; 0 = -y₁ + 5; ⇒ y₁ = 5
y₂ = 0; x₂ = 0 + 5; ⇒ x₂ = 5
ответ: две точки с координатами F(0; 5) и K(5; 0)
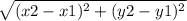 , где (х1; у1) - координаты начала отрезка, (х2; у2) - координаты конца отрезка.
, где (х1; у1) - координаты начала отрезка, (х2; у2) - координаты конца отрезка.
1). АВ = ВС = (25,6 - 9,6) / 2 = 8 (см)
2). Рассмотрим треугольник АВН, где ВН - высота треугольника, проведенная к основанию, значит, и медиана. АН = АС / 2 = 9,6 / 2 = 4,8 (см).
По теореме Пифагора
3). ВН, СК и АF - высоты треугольника, пересекаются в т. О. Найдем расстояние АО. Для этого найдем сначала АF.
4).
5). Треугольники АОН и ACF подобны по двум углам (углы в 90 градусов и общий острый угол при вершине А).
ответ: 6 см.