Значит раз трапеция прямоугольная, то боковая сторона является высотой и она будет 8 см по условию. проведем перпендикуляр из другой точки, параллельного высоте трапеции. он тоже будем равен 8, т.к. образует прямоугольник. получается прямоугольный треугольник, у которого одни катет равен 8. теперь маленькое основание возьмем за Х, а большое получается Х+6. вернемся к прямоугольному треугольнику. их большого основания вычитаем малое, это мы можем сделать, потому что, как я уже говорила, был образован прямоугольник, а противоположные стороны равны. Из Х+6 вычитаем Х, получаем 6. значит второй катет треугольника равен 6. теперь ищем гипотенузу у этого треугольника, она является боковой стороной и трапеции. по теореме пифагора 6 в кв+8в кв=100. гипотенуза будет равна 10. теперь ищем основания. вычисляем площадь у трапеции. одна вторая умн на (Х+6+Х) умн на 8=120. отсюда Х=12. это малое основание. а большое равно 12+6=18. все)
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника.
Пусть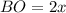 см и
см и 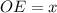 см, тогда
см, тогда 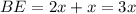 , что по условию он равен 9 см.
, что по условию он равен 9 см.
Следовательно,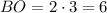 см и
см и 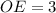 см
см
Аналогично, пусть теперь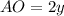 см и
см и 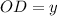 , тогда
, тогда 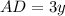 и по условию равен 12 см
и по условию равен 12 см
Таким образом,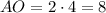 см и
см и 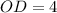 см.
см.
По условию медианы треугольника AD и BE взаимно перпендикулярны, следовательно
По теореме Пифагора из прямоугольного треугольника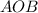
По теореме Пифагора из прямоугольного треугольника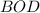
Тогда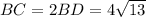 см
см
Из прямоугольного треугольника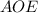 по теореме Пифагора
по теореме Пифагора
Тогда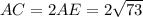 см
см
ответ: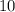 см;
см; 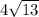 см;
см; 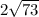 см.
см.