
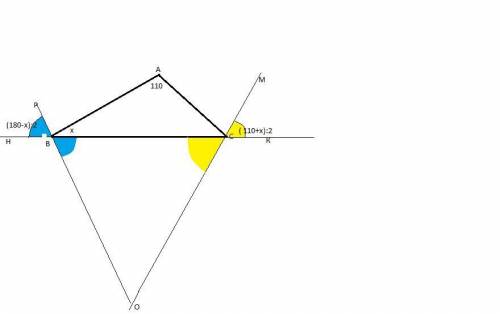
Прямые, содержащие биссектрисы внешних углов при вершинах В и С треугольника АВС, пересекаются в точке О.Найдите угол ВОС, если угол А равен 110 градусов.
Объяснение:
Пусть угол ∠АВС=х°, тогда для ΔАВС :
-внешний угол при вершине С, по т.о внешнем угле, равен ∠АСК=110°+х ,а ∠МСК=(110°+х) :2 , т.к СМ-биссектриса.
-весь внешний угол при вершине В равен (180°-х) , а его половина (180°-х):2.
Для ΔВОС : ∠В=∠РВН=(180°-х):2 как вертикальные;
∠С=∠МСК=(110°+х):2 как вертикальные.
По т. о сумме углов треугольника :
∠ВОС =180-(180°-х):2-(110°+х):2 или
∠ВОС =180-90°+х/2-55°-х/2 =35°
ответ ∠ВОС=35°
Объяснение:
1. Треугольники ACO и ABO равны. ОА - биссектриса угла => ∠BAC = 2*∠CAO. ∠CAO из прямоугольного треугольника определяется так: отношение противолежащего катета OC (к углу CAO) к гипотенузе OA есть синус этого угла. sin(∠CAO) = OC/OA = r/(2r) = 1/2. Угол, синус которого равен одной второй известен. Это угол в 30 градусов. Тогда ∠BAC = 2*30° = 60°.
2. Отрезки AB и AC равны. Т.к. отрезки касательных проведенных из одной точки к некоторой окружности равны. А именно AB = AH и AC = AH. Отсюда следует, что AB = AC.
3. Аналогично предыдущему вопросу доказываем, что CM = CE, CA = CB. AM = CM - CA, BE = CE - CB = CM - CA = AM.
UPD: Не синус одной второй равен 30 градусам, а синус 30 градусов равен одной второй. Или с применением арксинуса: арксинус одной второй равен 30 градусам. Описка незначительная.
8
Объяснение:1.По свойству касательных (две касательные к одной окружности,проведенные из одной точки равны) АВ=АС.ФС=ФЕ,ЕД=ДВ.
2. Р=АО+ОФ+ФА. ФД=2ДВ, АВ=АД+ДВ, можно записать, что Р=2АД+2ДБ,следовательно АВ= Р/2, 16/2=8 см