АД =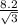 
Периметр ΔАОД = 8,2√3
Объяснение:
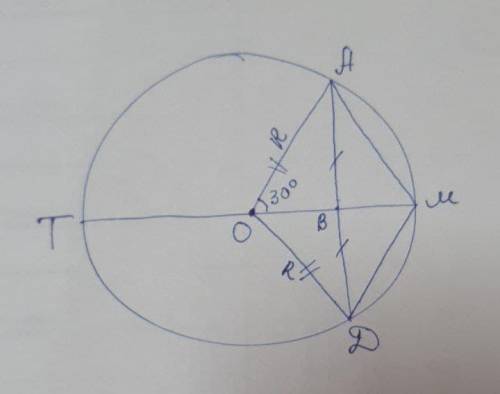
ΔАОД - равнобедренный (ОА=ОД=R), т.к. АВ=ВД (В - середина АД), то ОВ - медиана. Медиана в равнобедренном Δ является также высотой ⇒ОМ⊥АД.
Четырёхугольник АОДМ: Диагонали перпендикулярны, а если диагонали выпуклого четырехугольника взаимно перпендикулярны, то суммы квадратов его противолежащих сторон равны:
АО²+ДМ²=ОД²+АМ²
АО=ОД=R ⇒ R²+ДМ²=R²+АМ²
⇒ДМ=АМ ⇒ Четырёхугольник АОДМ - ромб,
ОА=ОД=ДМ=АМ=R
Рассмотрим ΔАОВ(∠В=90°). ОВ=1/2ОМ (св-во диагоналей ромба)
ОМ=1/2 ТМ ⇒ ОВ=1/4 ТМ = 1/4* 16,4 = 4,1 см
∠О=30°.
ОА=R=ОВ/cos 30° =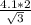 
=
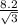
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
АВ=1/2 ОА = 1/2 * =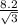 
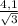, т.к. В - середина АД, то
АД = 2*АВ=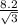
Периметр ΔАОД = 2*ОА+АД= 2*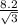 + 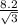= 8,2√3
1) Пусть точка C - точка пересечения отрезков AB и MK.
Тогда по первому признаку равенства треугольников (две стороны и угол между ними) будут равными треугольники AKC и CBM.
А значит и углы тругольников AKС и СMB равны. Из этого следует, по теореме о параллельных прямых, так как накрест-лежащие углы (AKС и СMB) равны, то отрезки AK и MB параллельны.
2) См. рисунок.
Так как CH- биссектриса, то углы KCH и HCT равны между собой и равны половине угла KCP, т.е. 29°.
Так как CK и TH параллельны, то накрест-лежащие углы KCH и CHT равны, также 29°.
Угол CTH = 180 - HCT - CHT =180-29-29=122°.
Таким образом углы в треугольнике CHT: 29, 29, 122.