Сторона ромба равна 10 см, острый угол равен 30°. Найдите радиус вписанной в ромб окружности
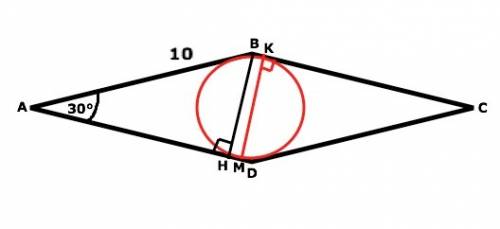
Стороны ромба равны между собой и являются касательными к вписанной окружности, центром которой является точка пересечения диагоналей ромба. Диаметр этой окружности, проведенный в точки касания, перпендикулярен обеим сторонам ромба (свойство диаметра).
Высота ВН противолежит углу 30°⇒
ВН равна половине гипотенузы. ВН=АВ:2=5 см
КМ⊥ВС и АD; ВН ⊥BC и АD⇒ КМ║ВН и равны, как перпендикуляры между параллельными прямыми. ⇒
d=5 cм, r=2,5 см
----------
Полезно запомнить: Диаметр вписанной в ромб окружности равен его высоте.
Образовавшийся прямоугольный треугольник будет равнобедренным с углами при основании по 45 градусов ( т.к. биссектриса делит угол прямоугольника пополам).Значит его катеты равны по 12 см ( либо по 8 см).Следовательно , вторая сторона прямоугольника равна 12 см ( или 8 см).
ответ: 20см,20см,12 см,12см.
или 20см,20см,8см,8см.