36π
Объяснение:
V = 4/3 πR³ R³ = (36π × 3)/4π = 27 R = 3
S = 4 πR²
S = 4π × 3² = 36π
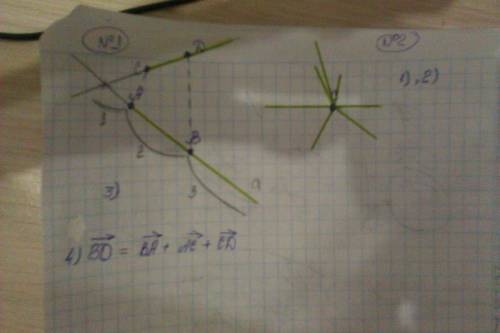
Как ни странно, расстояние между серединами АС и СВ, равно 19 см.
Пусть точка Т- середина АС, она делит отрезок АС на два равных отрезка длиной 9 см каждый, точка Р- середина СВ, тоже делит отрезок на два равных, по 10 каждый, тогда расстояние от точки Р до точки Т равно 9+10=19
2. Биссектриса АД делит угол ВАС пополам, по 40° равны и угол ВАД и угол ДАК
Так как АВ║ДК, при секущей АД углы ВАД и АДК равны, как накрест лежащие при указанных прямых и секущей, значит, угол АДК=40°, а угол АКД =180-40-40=100/град./
3.Раз треугольник равнобедренный, то ДМ не только биссектриса, но и медиана, но тогда периметр треугольника АВС =2*АД+2*АМ=
2*(АД+АМ)=22, а периметр треугольника АСМ =АД+АМ+ДМ=22/2+ДМ=
11+ДМ=16, откуда ДМ=5/см/
4.Значит, угол при основании х, а при вершине 10х,
х+х+10х=180; 12х=180
х=180/12=15
Углы при основании по 15 град., а при вершине 150 град.
5.Угол А равен 44=180-угол В- угол С, тогда сумма углов В и С равна 180-44=136, но угол Е равен 180 минус половины углов В и С , т.е. 180-(136/2)=180-68=112/град./
6.Медианы пересекаются в одной точке и делятся в ней в отношении 2/1. начиная от вершины. Значит, АЕ=5+2.5=7.5
И т.к. дан равносторонний треугольник, то расстояние от В до АС- длина перпендикуляра ВД, т.к. медиана будет и высотой. Тогда ВД=7.5/ см/
7.Нет. не существует. Если первая равна х, вторая 2х. третья х-1, то х+2х+х-1=47.
4х=48
х=12. Первая 12, вторая 24, третья 11, но сумма 12+11 меньше 24, не выполняется неравенство треугольника. Значит. такой треугольник нельзя построить.
8.Самый большой угол в этом треугольнике прямой. биссектриса делит его на два по 45 град., если в треугольнике, образованном высотой и катетом, найти острый угол, он будет равен 45-17=28, и теперь надо найти второй. отнять от 90-28=62град, получим угол искомого треугольника, тогда другой угол искомого треугольника равен 90-62=28 град., т.к. сумма острых углов в прямоугольном треугольнике равна 90 градусов.
Требуется по известному объёму шара, равного 36 * π см3, определить площадь поверхности сферы, которая ограничивает этот шар.
Как известно, объём шара (V) при известном радиусе R, вычисляется по формуле V = (4/3) * π * R3.
Согласно условия задания, имеем, (4/3) * π * R3 = 36 * π см3, откуда R3 = (36 * π см3) : ((4/3) * π) = 27 см3.
Последнее равенство позволяет определить длину радиуса шара (что тоже самое, длину радиуса сферы, которая ограничивает шар): R = 3 см.
Теперь легко вычислить площадь (S) поверхности сферы по формуле: S = 4 * π * R2 .
Имеем: S = 4 * π * R2 = 4 * π * (3 см)2 = 4 * π * 9 см2 = 36 * π см2 .
ответ: 36 * π см2.