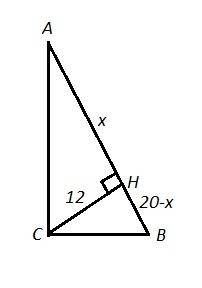
Если высота СН прямоуг. ΔАВС равна 12 см ,то гипотенуза АВ не может равняться 20 см.
По свойству высоты, проведённой из прямого угла прямоуг. треуг-ка на гипотенузу, она есть среднее пропорциональное (среднее геометрическое) между проекциями катетов на гипотенузу, то есть CH²=AH·BH .
Если гипотенуза АВ=20 см, то АВ=АН+ВН=20 см .
Обозначим АH=х , тогда ВН=(20-х) см.

Уравнение не имеет действительных корней, значит не существует треугольника с гипотенузой 20 см и высотой, проведённой из вершины прямого угла , равной 12 см.
Пусть у нас есть квадрат ABCD
и прямоугольник EBFG. Вершины B прямоугольника и квадрата совпадают. Сразу оговоримся, что именование вершин фигур начинается с левого верхнего угла и продолжается по порядку по часовой стрелке.
Нам известно что AB = BC = CD = DA = 10 см., EB = FG = 3см., BF = GE = 4 см.
Тогда от сюда следует что новая фигура, образовавшаяся после выреза прямоугольника (AEGFCD) будет иметь следующие размеры:
AE = AB - EB = 10 - 3 = 7см.
EG = GE = 4 см.
GF = FG = 3 см.
FC = BC - BF = 10 - 4 = 6 см.
CD = 10 см.
DA = 10 см.
Ссумируем 7 + 4 + 3 + 6 + 10 + 10 = 40 см.
ответ 40 см.