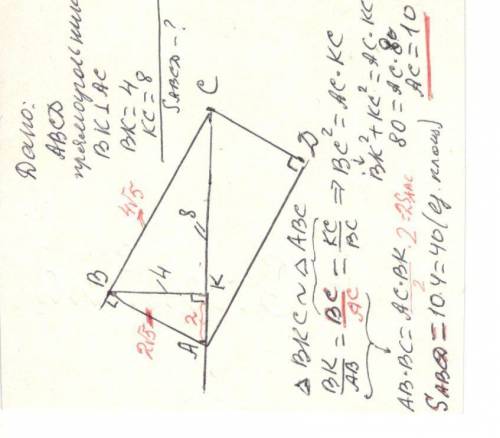
В прямоугольнике ABCD из вершины B опущен перпендикуляр BK на диагональ AC. Найдите площадь прямоугольника, если BK = 4 , KC= 8
"Решение"
* * * Cразу можно написать: BC² = AC *KC _ пропорциональные отрезки в прямоугольном треугольнике * * * A если . . .
ΔBKC ~ΔABC ⇒ BK/AB = BC / AC = KC/BC ⇔ BC² = AC *KC , но
BC² = BK²+ KC² =4² +8² =80 (теорема Пифагора)
80 =AC*8 ⇒AC =10
BK/AB = BC / AC ⇔ AB *BC = AC*BK ⇔ S(ABCD) = AC*BK =10*4= 40 (ед. площади) || S(ABCD) =2*AC*BK/2 =2S(ABC) ||
S(ABCD) = AC*BK =10*4= 40 (ед. площади)
Противоположные углы параллелограмма равны между собой, сумма соседних углов равна 180°. ∠A=∠C; ∠B=∠D; ∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°, если острый угол параллелограмма равен 52°, тогда остальные равны по: ∠А=52°; ∠В=∠D=180°-52°=128°; ∠A=∠C=52°; ∠B=∠D=128°.
Проверка: Сумма всех углов четырёхугольника равна 360°, то есть, должно выполниться равенство: ∠А+∠В+∠С+∠D=52°+128°+52°+128°=180°+180°=360°, равенство выполнено, значит, углы найдены верно. ответ: углы параллелограмма равны: 52°; 128°; 52°; 128°.