Гомотетия является преобра
зованием подобия.Коэффи
циент гомотетии "k" есть ко
эффициент подобия, равный
"k".
Любые два неравных парал
лельных отрезка гомотетич
ны друг другу. Есть две гомо
тетии, переводящие один от
резок в другой:
1) с коэффициентом k;
2) с коэффициентом -k.
Коэффициенты гомотетий
равны по модулю, но проти
воположны по знаку.
Если параллельные отрезки
равны, то |k|=1.
Если коэффициент гомоте
тии равен 1, то имеем тож
дественное преобразование:
образ каждой точки совпада
ет с ней самой. Тогда каждый
отрезок отображается сам на
себя. Не подходит. Нужно, что
бы один отрезок отображался
в другой
Если k=1 , то один отрезок отоб
ражается в другой параллель
ным переносом ( а это движе
ние, а не гомотетия) .
Остается: k= -1
Для равных параллельных от
резков есть только ОДНА го
мотетия k= -1 , переводящая
один отрезок в другой (это
центральная симметрия или
поворот на 180°).
Найти скалярное произведение векторов AK̅̅̅̅ и BL̅̅̅̅, если AK и BL − медианы равнобедренного треугольника ABC, площадь которого равна S, а угол ∠ А = 120°.
Объяснение:
1) ΔАВС-равнобедренный , ∠А =120°, АС=АВ=х ,∠В=∠С=(180°-120°):2=30° . Площадь треугольника равна половине произведения двух сторон на синус угла между ними. По условию она S.
S=1/2*х*х*sin120 ⇒ х²= 2S: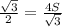
. х= 
.
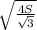По т. синусов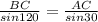
, 
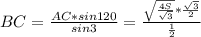, BC=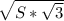
.
2) Используя правила сложения векторов :
вектор АК=0,5(АВ+АС), вектор ВL=0,5(ВА+ВС). Тогда
Векторы АК*ВL=0,25(АВ*ВА +АВ*ВС +АС*ВА +АС*ВС) .
Посчитаем каждое скалярное произведение
Вектора АВ*ВА=|АВ|*|ВА|*cos180=(4S/√3)*(-1)=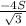
Вектора АВ*ВC=|АВ|*|ВC|*cos150=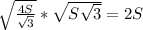
Вектора АС*ВА=|АС|*|ВА|*cos60=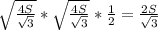
Вектора АC*ВС=|АC|*|ВС|*cos30=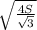
*
*
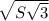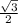=S√3 .
Для определения угла между векторами, вектора переносились для совмещения начал векторов.Использовались свойства углов параллелограмма, смежных углов ( см. чертеж)
АК*ВL=0,25*S(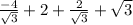
) =
.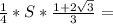
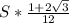