Объяснение:
Итак, когда секущая пересекает параллельные прямые, образуется несколько видов углов:
1) Внутренние накрест лежащие (которые равны)
2) Внутренние односторонние углы(их сумма составляет 180 градусов)
3) Соответственные углы(они равны)
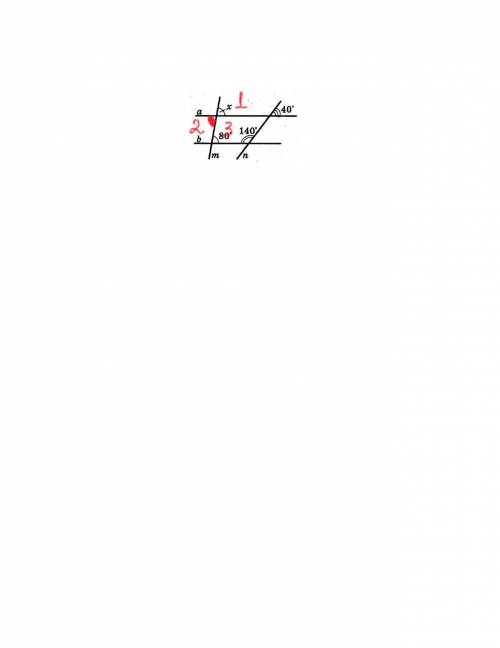
Я отметил на рисунке угол x как угол 1.
Угол 1 будет равен углу 2, т.к. они вертикальные, а это значит, что угол 2 будет равняться x.
А угол 3(который имеет градусную меру в 80 градусов) будет равен углу 2, так как они накрест лежащие. А это значит, что угол x будет равен 80 градусов.
Задача решена.
Объяснение:
Итак, когда секущая пересекает параллельные прямые, образуется несколько видов углов:
1) Внутренние накрест лежащие (которые равны)
2) Внутренние односторонние углы(их сумма составляет 180 градусов)
3) Соответственные углы(они равны)
Я отметил на рисунке угол x как угол 1.
Угол 1 будет равен углу 2, т.к. они вертикальные, а это значит, что угол 2 будет равняться x.
А угол 3(который имеет градусную меру в 80 градусов) будет равен углу 2, так как они накрест лежащие. А это значит, что угол x будет равен 80 градусов.
Задача решена.

Прямая а может лежать в одной из плоскостей (например, на рис. 2 в плоскости β), тогда другую плоскость она пересекает.
Прямая b может не лежать ни в одной из плоскостей, тогда она параллельна каждой. (рис. 3)
Прямая b может лежать в одной плоскости (например, на рис. 4 в β), тогда она параллельна другой плоскости.
Но пересекать плоскости прямая b не может.
Взаимное расположение прямых а и b однозначно определить нельзя. Они могут быть скрещивающимися или пересекаться. Но не могут быть параллельны.
2. Любые три точки, не лежащие на одной прямой, задают единственную плоскость.
Пусть точки А, В и С лежат в одной плоскости.
АВ⊂α, DC∩α = C, C∉AB ⇒ АВ и CD - скрещивающиеся.
К - середина AD, Р - середина СВ. КР = 3 см.
Проведем КТ║АВ и ТР║CD. Тогда угол между прямыми КТ и ТР будет равен углу между прямыми АВ и CD.
КТ - средняя линия ΔABD ⇒ КТ = АВ/2 = 3 см
ТР - средняя линия ΔСBD ⇒ ТР = CD/2 = 3 см
ΔКТР равносторонний, значит ∠КТР = 60°, значит и угол между прямыми АВ и CD равен 60°