
1.
М - середина АВ, значит МВ = АВ/2
Р - середина МВ, значит РВ = МВ/2 = АВ/4
К - середина ВС, значит КС = ВС/2
Е - середина КС, значит ЕС = КС/2 = ВС/4
N - середина АС, значит NA = АС/2
G - середина NA, значит GA = NA/2 = AC/4
По условию
PB + EC + GA = 12
АВ/4 + ВС/4 + АС/4 = 12
1/4 · (АВ + ВС + АС) = 12
АВ + ВС + АС = 12 · 4 = 48 (см)
2.
Из решения первой задачи следует, что
АР = 3/4 АВ
ВЕ = 3/4 ВС
CG = 3/4 AC
По условию
AP + BE + CG = 108
3/4 АВ + 3/4 ВС + 3/4 АС = 108
3/4 · (АВ + ВС + АС) = 108
АВ + ВС + АС = 108 · 4/3 = 144 (см)
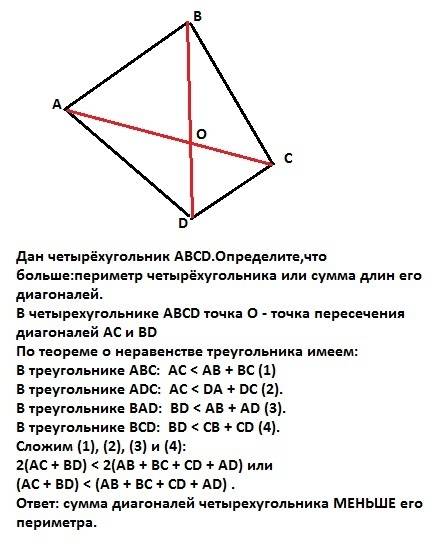
См. Объяснение
Объяснение:
Задание 2
Найти ∠АВС (рис. 675).
Решение
Теорема: вписанный угол равен половине дуги, на которую он опирается.
Вписанным называется угол, вершина которого лежит на окружности. ∠АВС - вписанный, так как его вершина В лежит на окружности.
Чтобы найти вписанный ∠АВС, надо найти градусную меру дуги АDС, на которую он опирается, а затем полученное значение разделить на 2.
Из рис. 675 следует, что вся окружность (360 градусов) разбита на две дуги: дугу АВС, на которую опирается угол АDС, и дугу АDС, на которую опирается угол АВС.
1) Находим градусную меру дуги АВС:
Дуга АВС = ∠АDС · 2 = 50° · 2 = 100°.
2) Находим градусную меру дуги АDС:
Дуга АDС = 360° - Дуга АВС = 360° - 100° = 260°.
3) Находим угол АВС:
∠АВС = Дуга АDС : 2 = 260° : 2 = 130°.
ответ: ∠АВС = 130°.
Задание № 3 (рис. 676)
Найти ∠А и ∠С.
Решение.
1) АОВ - диаметр.
2) Диаметр делит окружность пополам. Значит, дуга АВ, на которую опирается угол С, равна:
Дуга АВ = 360° : 2 = 180°.
3) Угол С равен половине дуги АВ:
∠С = Дуга АВ : 2 = 180° : 2 = 90°.
4) Так как ∠С = 90°, то это значит, что треугольник АВС - прямоугольный, и угол А равен:
∠А = 90° - ∠В = 90° - 37° = 53°
ответ: ∠А = 53°; ∠С = 90°.