В равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его медианы. Тогда треугольники AKB и ALB равны по второму признаку равенства треугольников. У них сторона AB общая, стороны AL и BK равны как половины боковых сторон равнобедренного треугольника, а углы LAB и KBA равны как углы при основании равнобедренного треугольника. Так как треугольники равны, их стороны AK и LB равны. Но AK и LB - медианы равнобедренного треугольника, проведённые к его боковым сторонам.
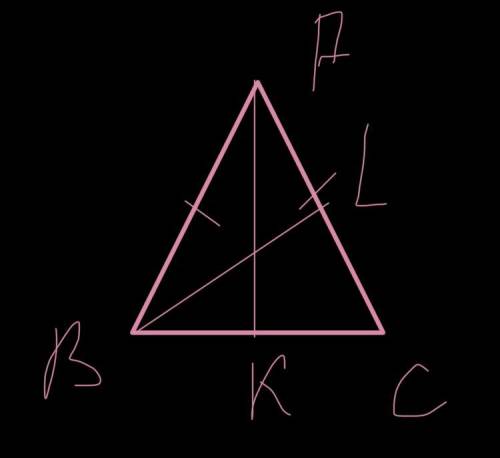
Объяснение:
По определению, две прямые параллельны, если существует плоскость в которой лежат две эти прямые, и они там параллельны. Отметим на данной прямой точки A и B. А точку обозначим как O. Пусть через точку О проходят две прямые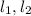
параллельные AB. Пусть 
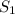-- плоскость, содержащая одновременно 
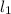и AB (эта плоскость существует из определения). Аналогично определяем плоскость 
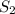. Заметим, что 
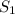и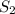 
проходят через точки O, A, B. Но по аксиоме через три точки, не лежащие на одной прямой проходит только одна плоскость. Значит плоскости 
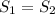= S совпадают. (назовём их общим именем S). Рассмотрим плоскость S: в ней лежат точки O, A, B и две прямые 
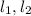. Причем, 
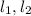проходят через точку O и параллельны AB. Но по аксиоме планиметрии (напомню, мы сейчас живем в плоскости S для которой выполнены все аксиомы планиметрии) через точку O может проходить лишь одна прямая, параллельная AB. Значит 
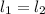, ч.т.д.