ответ: 52,3м; 104,6м
Объяснение:
Сам монумент, расстояние от точки А до основания монумента и расстояние от точки А до самой высокой точки образуют прямоугольный треугольник.
Высота монумента является катетом, расстояние от основания до точки А вторым катетом, а расстояние от точки А до вершины монумента гипотенузой.
Для того чтобы найти расстояние от точки А до вершины, нужно выстоу монумента разделить на sin60° и получим:
91/0,87=104,6м
Для нахождения расстояния от основания монумета до точки А, нужно расстояние от точки А до самой высокой точки умножить на cos60°: 104,6*0,5=52,3м
Диагональ призмы образует угол 45° с диагональю основания, т.к. диагональ основания - проекция диагонали призмы на плоскость основания и, значит, треугольник, в котором высота призмы и диагональ основания - катеты, прямоугольный равнобедренный, в нем диагональ основания равна тоже 20 см. ( т.к. углы при основании этого треугольника по 45°), диагональ квадрата равна а√2, где а - сторона квадрата, поэтому 20=а√2, откуда а=20/√2=10√2/см/. Площадь поверхности состоит из боковой поверхности и двух площадей основания. т.е. 4а*Н+2а²=4*10√2*20+(10√2)²=800√2+400=
(400*(2√2+1))/см²/
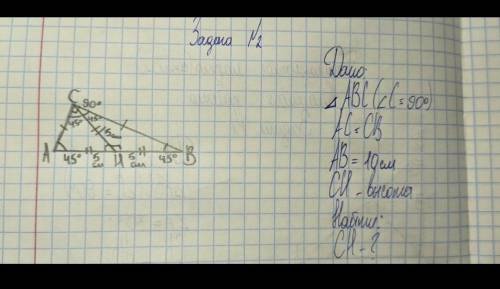
Треугольник АВС прямоугольный равнобедренный,т к по условию задачи АС=СВ,из этого следует,что
<А=<В=45 градусов
Так как треугольник равнобедренный,то высота является и медианой-делит основание АВ пополам
10:2=5 см
А также высота является биссектрисой-разделила угол С на два равных угла
90:2=45 градусов
Высота разделила треугольник АВС на два равных треугольника
Они тоже равнобедренные и прямоугольные,т к
<СНА=90 градусов
<А=<АСН=45 градусов
Если равны углы при основании,значит равны и боковые стороны
АН=СН=5 см
У вас,кстати ,на чертеже против СН написано 5 см
Объяснение: