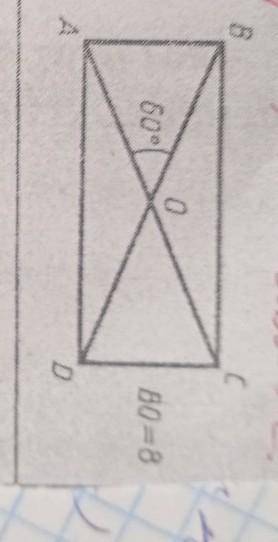
Если один из углов ромба равен 60°, второй равен 120° ( из суммы внутренних углов между параллельными прямыми и секущей). Поэтому его меньшая диагональ делит его на два равносторонних треугольника и равна стороне ромба.
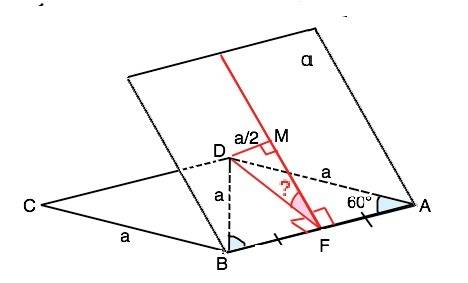
а) CВ║АВ, лежащей в плоскости α и, следовательно, параллельна этой плоскости (свойство). Расстояние от точки до плоскости равно длине перпендикуляра между ними. Все точки прямой, параллельной какой-либо плоскости, равноудалены от неё. ⇒ Расстояние от точки С до плоскости α равно расстоянию от точки D до неё, т.е. а/2.
б). Линейный угол двугранного угла определяется лучами, проведенными в гранях угла из одной точки ребра перпендикулярно ему.. На рисунке DF – высота ∆ АDВ. DF⊥АВ, DM перпендикулярна α, МF – проекция DF на плоскость α. По т.о 3-х перпендикулярах МF⊥АВ. Угол МFD – искомый.
в) DF⊥АВ, DF=a•sinDAF=a√3/2. Из ∆ DMF sinDFM=a/2:a√3/2.=1/√3
Определение: "Решение треугольника - исторический термин, означающий решение главной тригонометрической задачи: по известным данным о треугольнике (стороны, углы и т. д.) найти остальные его характеристики".
У треугольника общего вида имеется 6 основных характеристик: 3 линейные (длины сторон a , b , c) и 3 угловые ( α , β , γ ).
В нашем случае даны три стороны, значит надо найти три угла и этого достаточно, так как нет других указаний в условии.
Итак, имеем три стороны.
Углы находятся по теореме косинусов:
CosD=(DE²+DF²-EF²)/(2*DE*DF) или CosD=(25+64-16)/80 ≈ 0,9125
CosE=(DE²+EF²-DF²)/(2*DE*EF) или CosE=(25+16-64)/40 ≈- 0,575
CosF=(EF²+DF²-DE²)/(2*EF*DF) или CosF=(16+64-25)/64 ≈ 0,859.
По таблице находим углы:
<D≈ 24°
<E≈125°
<F≈ 31°
Проверка: 24°+125°+31°=180° сумма углов треугольника равна 180°.
Треугольник решен правильно.