
Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
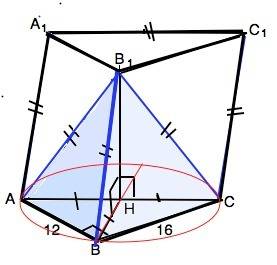
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.
ответ: после построения диагоналей ромб разбивается на 4 треугольника. диагонали ромба располагаются под прямым углом, то есть, треугольники, которые образовались, оказываются прямоугольными.
обозначим большую и малую диагонали ромба как d₁ и d₂, а углы ромба — а (острый) и в (тупой), теперь из формулы
tg a = 2/((d₁/d₂)-(d₂/d₁)) находим
tg a = 2/((2√3 /2)-(2/2√3)) = 2/(√3-1/√3)=
2/(√3-√3/3=2/(√3(1-1/3)= 2/(√3(2/3)=
2√3/2=√3
tg 60°=√3
углы ромба 60° и 120°
подробнее - на -
объяснение: