
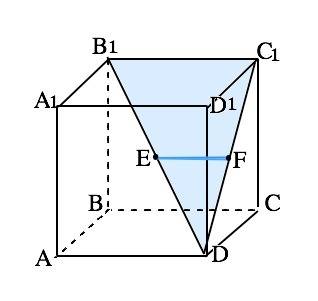
В ∆ В1DC1 отрезок EF соединяет середины сторон В1D и С1D, следовательно, EF- средняя линия и параллельна В1С1. Противоположные грани куба параллельны, противоположные стороны граней параллельны. ВС1 || А1D1, В1С1||ВС. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости. ⇒ В1С1 параллельна плоскостям АBCD и ADD1A1.
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо параллельна этой плоскости либо лежит в этой плоскости. EF параллельна В1С1,⇒ она параллельна АBCD и ADD1A1. EF параллельна В1С1, принадлежащей плоскости ВСС1В1 и А1В1С1D1, ⇒ прямая EF параллельна плоскостям четырех граней куба: АВСD. A1B1C1D1. AA1D1D, BB1C1C.
Найдем площадь треугольника АВС по формуле Герона или найдя по Пифагору высоту, опущенную на основание ВС.
а) По Герону. Полупериметр треугольника равен 33:2 = 16,5.
Sabc = √(16,5*6,5*6,5*3,5) = 6,5√57,75.
б) По Пифагору: Hbc = √(10²-6,5²) = √(16,5*3,5). =>
Sabc = (1/2)*13*√57,75 = 6,5√57,75.
Площадь треугольника АВС можно определить так:
Sabc = (1/2)*AB*CH или 6,5√57,75 =5*СН => СН = 1,3*√57,75.
Тогда из прямоугольного треугольника АСН по Пифагору:
АН = √(10² - (1,3*√57,75)²) = √2,4025 = 1,55.
ответ: АН = 1,55.