ответ: два решения (одно для остроугольного треугольника, другое для тупоугольного...)
1) Р = 256 (см)
2) Р = 56V21 (см)
Объяснение: треугольник АВС, основание ВС=2а (чтобы не возиться с дробями); АВ=АС=b
P = 2a+2b = 2(a+b)
а=b*cos(B); по т.синусов: b=2R*sin(B)
S = 2a*h/2 = ah; h = b*sin(B)
S = P*r/2 = (a+b)*r
(a+b)*r = ab*sin(B)
b(1+cos(B))*r = b*b*sin(B)*cos(B)
(1+cos(B))*r = 2R*sin^2(B)*cos(B)
r/(2R) = (1-cos(B))*cos(B)
обозначим х=cos(B)
x^2 - x + (6/25) = 0
(5x)^2 - 5*(5x) + 6 = 0
по т.Виета корни (3) и (2)
5х=3 ---> х = 0.6
---> sin(B) = V(1-0.36) = 0.8 или
5х=2 ---> х = 0.4
---> sin(B) = V(1-0.16) = 0.2V21
b = 2*50*0.8 = 80 или
b = 2*50*0.2V21 = 20V21
a = 80*0.6 = 48 или
а = 20V21*0.4 = 8V21
P = 2*(80+48) = 128*2 = 256 или
Р = 2*(20+8)*V21 = 56V21
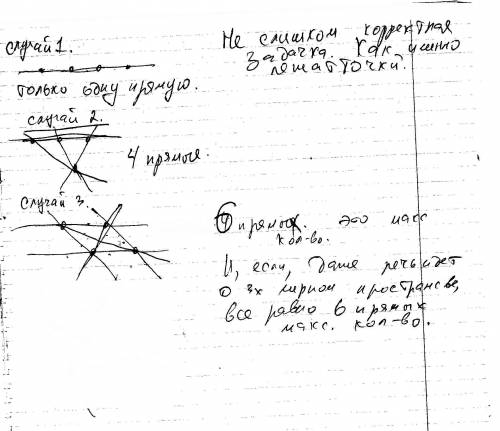
Диагональ делит угол пополам - эта диагональ - биссектриса.
Биссектриса трапеции отсекает от нее равнобедренный треугольник. В самом деле:
В треугольнике ВСД угол СВД=углу ВДА как накрестлежащие, угол ВДС=углу ВДА как половины угла АДС. Следовательно, угол ВДС=углу СВД.
ВС=СД.
В трапеции треугольники, образованные диагоналями и основаниями, - подобны. Они имеют по равному вертикальному углу при пересечении биссектрис и равные накрестлежащие углы.
k=AО:ОС=8:6
АД:ВС=8:6
Пусть коэффициент этого отношения равен х
Тогда АД=8х, ВС=6х
Опустим из С высоту СН=12.
АН=ВС, НД=8х-6х=2х, СД=ВС=6х
По т.Пифагора
СД²-НД²=СН²
36х²-4х²=144
32х²=144
х=√4,5=1,5√2 ⇒
ВС=9√2
АД=12√2
S (АВСД)=(21√2)*12:2=126√2 см²