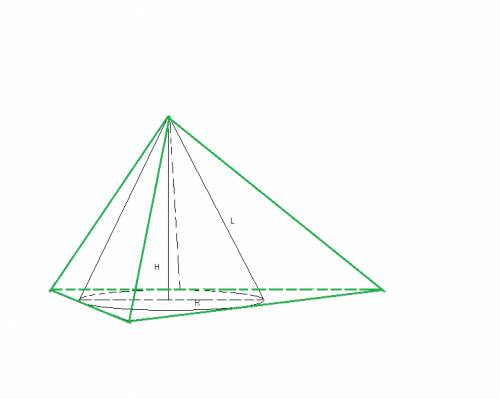
Пусть общая высота конуса и пирамиды равна Н.
Обозначим объемы конуса и пирамиды через V1 и V2 соответственно ,
а их боковые поверхности – через S1 и S2
тогда V1=1/3pi*R^3H , S1=pi*RL ,
где L-образующая конуса.
Найдем V2 и S2.
Так как периметр основания пирамиды равен 2р ,
а основание конуса – вписанная в основание пирамиды окружность,
то площадь основания пирамиды равна pR,
откуда V2=1/3pRH, S2=pL (высота любой грани равна L).
Тогда
V1 : V2 =1/3piR^2H : 1/3pRH = pi*R/p
S1 : S2 =pi*RL : pL = pi*R/p
ответ V1 : V2 = S1 : S2 = pi*R/p
Объяснение:
3. 1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания,
значит ∠ ОКМ=90°-7°=83° .
2) ∆ ОКМ- равнобедренный (ОК=КМ=r) , значит ∠ОКМ=∠ОМK=83°.
4. 1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания,
значит ∠ ОКМ=90°-84°=6°
2) ∆ ОКМ- равнобедренный (ОК=КМ=r) , значит ∠ОКМ=∠ОМK=6°.
5. ∠ ABC =90°(вписанный), т.к ∪ АС=180° (опирается на диаметр АС). Тогда ∠С=180°-90°-75°=25°
6. 1) ∪ AN=73°·2=146° (стягивает вписанный ∠ NBA). Тогда
∪ NB =∪ AB-∪AN=180°-146°=34°.
2) ∠NMB=34°/2=17° (вписанный не центральный угол)
7. 1) ∆ АОВ- равнобедренный(АО=ОВ=r), значит ∠ОАВ=∠АВО=15°. Тогда ∠ОВС =56°-15°=41°.
2) ∆ ВОС- равнобедренный(ВО=ОС=r), значит ∠ОВС=∠ВСО=41°.
8. ∆ АОВ =∆ СОD (AO=OD=r, CO=OB=r, ∠AОВ =∠CОD-вертикальные ), значит ∠ОАВ =∠ОСD=25°
...