№1
Рассмотрим треугольники FMN и FNK. Эти треугольники равны по первому признаку равенства треугольников(по двум сторонам и углу между ними). Сторона FK-общая,
сторона FM=NK, докажем это - по условию EF=EK (треугольник равобедренный), М-середина стороны EF, значит FM=1/2EF, N-середина ЕК, значит NK=1/2ЕК, значит FM=NK, а угол F=К, так треугольник FEK равнобедренный, то углы при основании равны. А так треугольники равны, то и все стороны у треугольников равны (третий признак равенства), значит сторона FN=KM
№2
В этой задачи перепроверь, что надо доказать, треугольника ЕРЕ не существует, уточни условие и я дорешаю.
1)Диагональ квадрата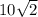
2)Такого правильного многоугольника не существует
3)Периметр ромба 60
Объяснение:
1)Сторона квадрата это два радиуса, то есть a = 2r = 2 * 5 = 10
По теореме Пифагора, диагональ =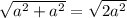 =
=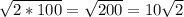 , где а - сторона квадрата
, где а - сторона квадрата
2) Сумма улов n-угольника s = 180(n - 2)
1600 = 180(n - 2);
1600 = 180n - 360;
1960 = 180n;
196 = 18n;
n = 10,8 а так как n не является натуральным числом то такого многоугольника не существует
3)Так ромб частный случай паралеллограмма то его диагонали точкой пересечения делятся пополам, а свойству ромба его диагонали перпендикулярны, тогда по теореме Пифагора a =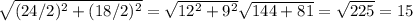
(a - сторона ромба )
По свойству ромба все его стороны равны тогда P ромба = 4a
= 4 * 15 = 60