10 МИНУТ ОСТАЛОСЬ!! На окружности с центром в точке O по порядку отмечены 4 точки: D, H, L, P. Найди вторую сторону получившегося четырёхугольника, если DH∥PL,DH=PL, радиус этой окружности 10 см, а DH=12 см.

10 МИНУТ ОСТАЛОСЬ!! На окружности с центром в точке O по порядку отмечены 4 точки: D, H, L, P. Найди

👇

Увидеть ответ

Ответ:

kulikovamascha

16.03.2020

12 см

Объяснение:

Задание

На окружности с центром в точке O по порядку отмечены 4 точки: D, H, L, P. Найти вторую сторону получившегося четырёхугольника, если DH∥PL,DH=PL, радиус этой окружности 10 см, а DH=12 см.

Решение

Так как все диагонали равны диаметру и в центре пересечения делятся пополам, а центральные углы, образованные радиусами, равны 90 градусам, то полученный четырёхугольник - квадрат.

Вторая сторона также равна 12 см.

ответ: 12 см

4,4(8 оценок)

Открыть все ответы

Ответ:

Anastasiia666

16.03.2020

остроугольный и равнобедренный.

Объяснение:

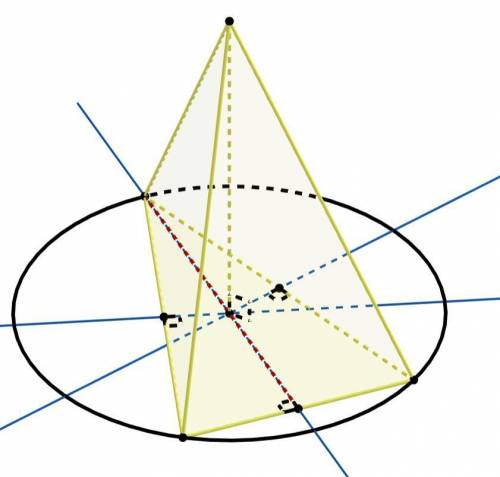
Если боковые рёбра пирамиды составляют равные углы с плоскостью основания, то основанием высоты пирамиды является центр окружности описанной около многоугольника из основания.

Центр окружности описанной около треугольника лежит внутри треугольника, если он остроугольный.

Так же этот центр лежит на пересечении серединных перпендикуляров к сторонам треугольника. Если центр описанной окружности лежит на одной высоте треугольника, то эта высота лежит на серединном перпендикуляре. А значит высота одновременно является и медианой. Тогда треугольник равнобедренный.

Основанием пирамиды является треугольник. Все боковые рёбра пирамиды с основанием образуют равные уг

4,7(21 оценок)

Ответ:

petechkaPetrovPetor

16.03.2020

Может быть не разными,а равными? Так ,мне кажется, правильнее. Равными называют треугольники элементы которого ( углы, стороны) соответственно равны. Ну если все таки разными , то: разными называют треугольники элементы которого ( углы, стороны) не равны . Но это странно звучит ...

Перпендикулярным отрезком, проведенным из точки к данному прямой называют перпендикуляром .

Теорема — утверждение, справедливость которого устанавливается путем рассуждения, а сами рассуждения — доказательством теоремы
Условие — это начало теоремы, а заключение — конец теоремы

Теорема о перпендикуляре , проведенным из точки к данной прямой: из точки, не лежащей на данной прямой, можно провести перпендикуляр к этой прямой, и притом только один

Медиана треугольника— это отрезок,соединяющий вершину треугольника с серединой противоположной стороны
Любой треугольник имеет три медианы.

Биссектриса треугодиника — отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны
Любой треугольник имеет три биссектрисы.

Высота треугольника — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Любой треугольник имеет три высоты.

Равнобедренным треугольником называется треугольник, у которого две его стороны равны.
Стороны равнобедренного треугольника называют боковыми сторонами.

Равносторонний треугольник — это треугольник, у которого все стороны равны.
Свойство : все углы равностороннего треугольника равны.

Теорема об углах равнобедренного треугольника: В равнобедренном треугольнике углы при основании равны.

Теорема о биссектрисе равнобедренного треугольника: в равнобедренном треугольнике биссектриса , проведенная к основнованию, является медианой и высотой.

Теорема о равестве треугольников: 1) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и уголу между ними другого треугольника, то такие треугольники равны.
2) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Окружность— геометрическая фигура, состаящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Данная точка — центр окружности.
Радиус — отрезок соединяющий центр окружности с какой либо точкой окружности.
Хорда — отрезок соединяющий две точки окружности
Диаметр — хорда проходящая через центр окружности

4,6(28 оценок)

Это интересно:

14.02.2021

Хочешь жить счастливо? Узнай, что для этого нужно!...

Взаимоотношения

21.07.2022

10 простых способов наладить отношения с подростком...

Дом-и-сад

24.10.2021

Унитаз забился или медленно сливает: как решить проблему за несколько минут...

Праздники-и-традиции

18.06.2022