Дано: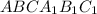 
- прямая призма, ABC
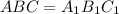- прявильные треугольники, AB = 10 см, 
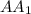= 13 см.
Найти: S пол.пов.
1) S полн.пов. = 2 * S оснований + 3 * S бок.пов.
2) ABC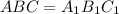 - прявильные треугольники (по условию), значит, все их стороны равны. Раз одна сторона равна 10 см, то каждая из остальные стороны равны 10 см.
Найдем площадь ABC. Для этого проведем высоту BH из вершины B (можно из любой вершины) в основанию, при этом высота будет являться и медианой, и биссектрисой одновременно, значит, AH=AC. Образовались два прямоугольных треугольника, рассмотрим треугольник ABH.
Т.к. AH=AC, то AH = 10:2=5 см.
По теореме Пифагора найдем BH:
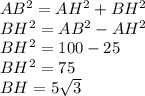
Теперь найдем площадь ABC:
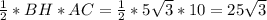кв.см.
2) Грани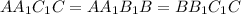 
т.к. призма прямая, и её грани - равные прямоугольники.
Найдем площадь любой из этих граней: 10*13=130 кв.см.
Тогда S бок.пов.=3*130=390 кв.см
3) S оснований =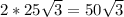 
кв.см.
4) S полн. пов. =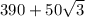 
кв.см.
ответ: 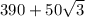кв.см.
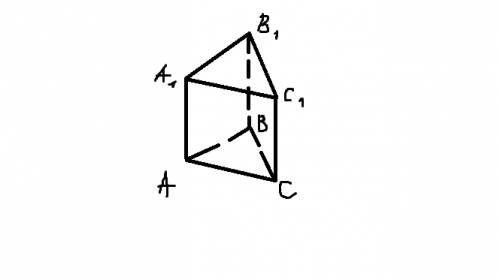
E ∈ AD
Sпол -?
Sпол = Sосн + Sбок .
Все грани с плоскостью основания составляют равны углы (в данном случае 60°),значит высота пирамиды проходит через центр O окружности вписанной в основании ABCD. Через точку O проведем прямую ,перпендикулярную AD (BC) ,которая пересекает сторону AD допустим в точке E ,а сторону BC в точке F. KE и KF будут апофемы соответственно боковых граней AKD и BKC.Из OE ⊥ AD⇒OE ⊥ KE
(теорема трех перпендикуляров). Треугольник EKF_равносторонний: (∠KEO=∠KFO=60°) . Поэтому KE=KF=EF || =2*OE =2*r||.
Из ΔKOE: KO =KE*√3/2 ⇒KE=2KO/√3 =2h/√3.
KE=KF=EF =2h/√3.
Найдем сторону основания.Из вершины B опускаем перпендикуляр BN на AD. EF =BN =AB/2 (катет против угла 30°)⇒ AB=2*EF.
---
Sосн =AB*BN =2*EF*EF =2EF² .
Sбок=4*(1/2)AD*KE=2AD*KE =2AB*KE =2*2*EF*KE =4EF².
Sпол = Sосн + Sбок =2EF²+4EF² =6EF²=6*(2h/√3)² =(6*4/3)h²=8h².
ответ: 8h².