ответ: 12 (ед. площади)
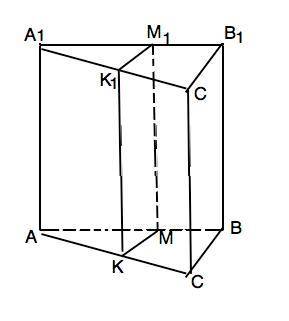
Объяснение: Площадь боковой поверхности призмы равна произведению высоты призмы на периметр основания: S=Н•Р=24
При проведении плоскости через среднюю линию основания параллельно боковому ребру плоскость сечения отсекает от оснований равные треугольники, подобные треугольникам оснований с коэффициентом подобия k=0,5а:а=1/2. Периметры подобных фигур относятся как их линейные размеры. Следовательно, S₂(бок)=Н•Р/2. Т.к. высота призмы не изменилась, S₂(бок)=24•1/2=12 (ед. площади)
Находим координаты точки С, симметричной точке А относительно точки Е.
х(С) = 2х(Е) - х(А) = 2*1 - 1 = 1,
у(С) = 2у(Е) - у(А) = 2*0 - 4 = -4. Точка С(1; 4),
Далее есть несколько вариантов нахождения площади параллелограмма.
1) Есть прямая формула по координатам точек треугольника АВС найти его площадь.
А площадь параллелограмма равна двум площадям треугольника АВС.
S(АВС)=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 24.
S(АВСД) = 2*24 = 48.
2) Можно сделать то же самое с применением формулы Герона для определения площади треугольника АВС.
Находим длины сторон:
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √ 85 ≈ 9,219544457.
ВC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √37 ≈ 6,08276253.
AC (в) = √((Хc-Хa)²+(Ус-Уa)²) = √64 = 8.
Периметр равен Р = 23,302307,
полупериметр р = 11,65115.
S(АВС) = √(p(p-a)(p-b)(p-c)) = 24.
S(АВСД) = 2*24 = 48.
3) площадь параллелограмма через стороны и угол А: S = absin A.
Угол находим по теореме косинусов после определения диагонали ВД.
Решение громоздкое.
4) площадь параллелограмма через диагонали и угол между ними.
Угол между диагоналями находится после определения их угловых коэффициентов. Тоже решение не простое.