1) Основание прямой призмы – прямоугольный треугольник с гипотенузой 15см и катетом 12см. Найдите площадь боковой поверхности, если грань содержащая больший катет – квадрат. Решение. По Пифагору найдем второй катет основания призмы: √(15²-12²)=√(27*3)=9см. Следовательно, больший катет равен 12см и высота призмы равна 12см (так как боковая грань - квадрат 12х12 - дано). Площадь боковой поверхности призмы равна Sб=P*h, где Р - периметр, а h - высота призмы. Sб=36*12=432см².
2) Ребро правильного тетраэдра равно а. Постройте сечение плоскостью, проходящей через ребро АС и делящее его в отношении 1:2, и проходящей параллельно ребру АВ. Решение. Условие для однозначного решения не полное. Во-первых, не понятно условие "Постройте сечение плоскостью, проходящей через ребро АС и делящее его в отношении 1:2". Проходящее - содержащее это ребро или пересекающее его? Раз сечение делит ребро в отношении 1:2, значит плоскость пересекает это ребро и делит его в отношении 1:2, но считая от какой вершины? Во вторых, таких сечений может быть бесконечное множество, так как плоскость, параллельная прямой АВ, может пересекать тетраэдр в любом направлении. Например, параллельно грани АВS (сечение MNP) или проходящее через точку Q на ребре AS (сечение MQDN). Причем линия пересечения грани АSB и плоскости сечения будет параллельна ребру АВ. Вывод: однозначного решения по задаче с таким условием нет.
11.
Дано:
ΔАВС - равнобедренный
АС = ВС = 13
АВ = 10
Найти:
АС - высоту. опущенную на боковую сторону
СD - высота равнобедренного треугольника. опущенная на основание, является и медианой. Поэтому AD = BD = 0.5AB = 0.5 · 10 = 5.
По теореме Пифагора
АС² = CD² + AD²
13² = CD² + 5²
CD² = 13² - 5² = 144 = 12²
CD = 12
Площадь треугольника АВС
S = 0.5 CD · AB = 0.5 · 12 · 10 = 60
Площадь треугольника АВС можно также вычислить и так:
S = 0.5 BC · AE
откуда
АЕ = 2S : BC = 2 · 60 : 13 = 9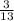
≈ 9.23
АЕ = 9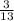
≈ 9.23
12.
Дано:
MKNR - ромб
KR = 10 - 1-я диагональ ромба
MN = 12 - 2-я диагональ ромба
Найти:
МК - сторону ромба
Пусть О - точка пересечения диагоналей ромба.
Диагонали ромба делятся точкой пересечения пополам, поэтому
КО = 0,5 KR = 0.5 · 10 = 5
МО = 0,5 MN = 0.5 · 12 = 6
Диагонали ромба пересекаются под прямым углом, поэтому
КО ⊥ МО и ΔМКО - прямоугольный с гипотенузой МК.
По теореме Пифагора
МК² = КО² + МО²
МК² = 5² + 6² = 61
МК = √61 ≈ 7,81
Сторона ромба МК =√61 ≈ 7,81