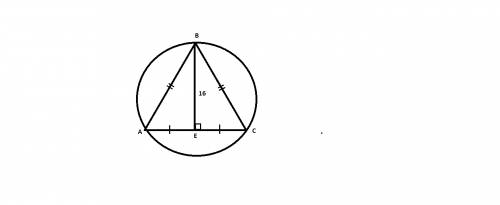
Высота, проведенная к основанию равнобедренного треугольника равна квадрату стороны деленная на 2радиуса описанной окружности: h=a^2/2R. Из этой формулы найдем длину стороны АВ треугольника АВС: a^2=2Rh=2*10*16 => a=корень из 320.
Чтобы найти площадь треугольника найдем длину половины основания, а затем и все основание (т к высота в равнобоком треугольнике это и медиана) по теореме пифагора (из прямоугольного треугольника АВЕ) АЕ=корень из 320-16^2=корень из 64=8см, тогда АС=8+8=16см.
Найдем площадь треугольника АВС=1/2*h*a; где h-высота, a-сторона, к которой проведена высота.
S=1/2*16*16=128cм^2
1) Поскольку sinα=1/2, значит гипотенуза в 2 раза больше катета. Значит надо построить треугольник с таким отношением.
Если брать конкретные значения, то пусть один из катетов прямоугольного треугольника равен AB=5 см, тогда гипотенуза AC=5*2=10 см.
2) Поскольку sinα=2/5, значит гипотенуза в 5/2=2,5 раза больше катета.
Если брать конкретные значения, то пусть один из катетов прямоугольного треугольника равен AB=4 см, тогда гипотенуза AC=4*2,5=10 см.
3) Поскольку sinα=0,6, значит гипотенуза в 1/0,6=10/6=5/3 раза больше катета.
Если брать конкретные значения, то пусть один из катетов прямоугольного треугольника равен AB=6 см, тогда гипотенуза AC=6*5/3=10 см.
4) sinα=0,7, значит катет в 0,7 раз меньше гипотенузы.
Если брать конкретные значения, то пусть гипотенуза AC=10 см, тогда катет AВ=0,7*10=7 см.