30° и 60°
Объяснение:
Теорема: внешний угол треугольника равен сумме двух других углов треугольника, не смежных с ним.
Обозначим углы треугольника ∠А, ∠В и ∠С = 90°, а внешние углы 12 х и 15 х. Составим систему уравнений и найдём х:
12 х = ∠А + ∠С = ∠А + 90°
15 х = ∠В + ∠С = ∠В + 90°
или
12 х = ∠А + 90° (1)
15 х = ∠В + 90° (2)
Сложим (1) и (2)
12х + 15х = ∠А + 90° + ∠В + 90°
А так как ∠А + ∠В = 90° (сумма острых углов прямоугольного треугольника равна 90°), то:
12х + 15х = 90° + 90° + 90°
27х = 270°
х = 270 : 27 = 10°
∠12 х = 12 · 10 = 120°
∠15 х = 15 · 10 = 150°
Так как:
12 х = ∠А + 90° (1)
15 х = ∠В + 90° (2)
то заменим полученные значения 12 х на 120° и 15 х на 150° и найдём острые углы треугольника:
120° = ∠А + 90°, откуда ∠А = 120° - 90° = 30°
150° = ∠В + 90°, откуда ∠В = 150° - 90° = 60°
ответ: 30° и 60°.
Дано :
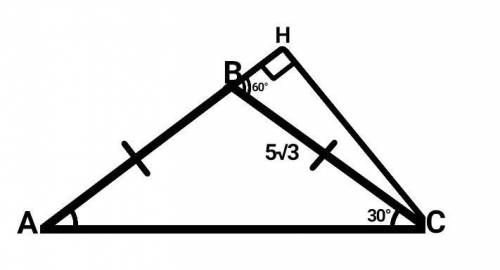
∆АВС — равнобедренный (АС — основание).
АВ = ВС = 5√3.
<С = 30°.
СН — высота.
Найти :
СН = ?
В равнобедренном треугольнике углы при основании равны.Следовательно —
<А = <С = 30°.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.То есть —
Внешний <В = <А + <С
Внешний <В = 30° + 30°
Внешний <В = 60°.
Рассмотрим прямоугольный ∆ВСН (СН лежит вне треугольника, так как ∆АВС — тупоугольный).
BC — гипотенуза (так как лежит против угла в 90°).
Тогда —
Sin(<HBC) = CH/BC (по определению синуса острого угла прямоугольного треугольника)
Sin(60°) = CH/(5√3)
Обозначим СН за х.
Тогда —
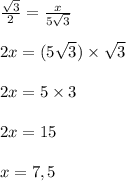
СН = 7,5 (ед).
7,5 (ед).
— — —
Надеюсь, я Вам. Есть вопросы по поводу решения? Задавайте в комментариях.
Р АВО= 7+12:2+14:2=20
Р ВОС= 11+7+6=24