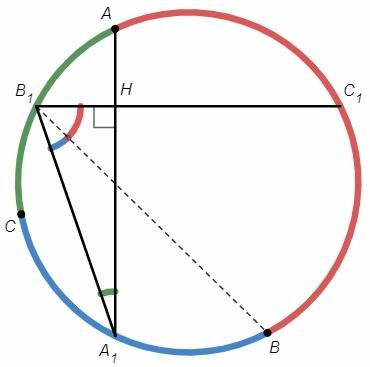
Вершины △ABC разбивают описанную окружность на три дуги. Биссектрисы углов треугольника делят эти дуги пополам (два равных вписанных угла опираются на равные дуги), точки A1, B1, C1 - середины дуг.
Вписанные углы ∠BB1C1, ∠BB1A1, ∠A1 опираются на половины дуг AB, BC, AC, следовательно сумма вписанных углов равна четверти окружности, 90.
∠BB1C1+∠BB1A1+∠A1 =∪AB/4+∪BC/4+∪AC/4 =360/4 =90
AA1 и B1C1 пересекаются в точке H. В △A1B1H сумма углов ∠A1 и ∠B1 равна 90, треугольник прямоугольный, AA1 и B1C1 пересекаются под прямым углом.
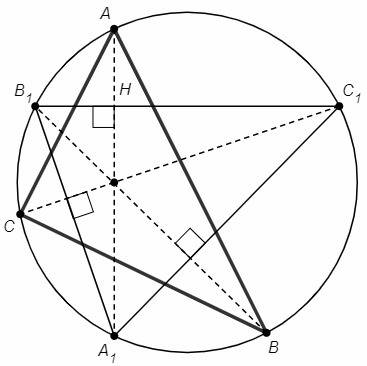
Аналогично BB1⊥A1C1, CC1⊥A1B1. Биссектрисы △ABC являются высотами △A1B1C1. Центр вписанной окружности (пересечение биссектрис) △ABC является ортоцентром (пересечением высот) △A1B1C1.
Точка пересечения биссектрис АМ и ДМ, очевидно, находится на стороне ВС.
Угол АМВ = угол МАД (накрест лежащие углы для параллельных ВС и АД, секущей АМ) , угол АМВ = угол МАД (так как АМ - биссектриса) .
Треугольник АВМ равнобедренный, АВ = ВМ.
Угол СМД = угол АДМ (накрест лежащие углы для параллельных ВС и АД, секущей ДМ) , угол АДМ = угол СДМ (так как ДМ - биссектриса) .
Треугольник СМД равнобедренный, СМ = СД.
АВ = СД (противоположные стороны параллелограмма) .
Поэтому АВ = ВМ = СМ, ВС = ВМ + СМ = 2*АВ.
Периметр 2*(АВ + ВС) = 2*3*АВ = 36 см.
АВ = 6 см, ВС = 12 см.
Диагональ образует со сторонами прямоугольный треугольник и является его гипотенузой. Против угла в 30 градусов лежит катет равный половине гипотенузы.
Следовательно первая сторона равна a = 6*tg30°= 6*√3/3 = 2√3cм
Площадь S = a*b = 6*2√3 = 12√3 cм²
Один из углов между основанием и диагональю равен (180-120)/2 = 30°
следовательно мы имеем треугольник аналогичный треугольник, у которого одна из сторон в √3 раз больше другой. S = a²√3
a*b = a²√3 = 2√3м²
a = √2 м
в = √2*√3 = √6 м