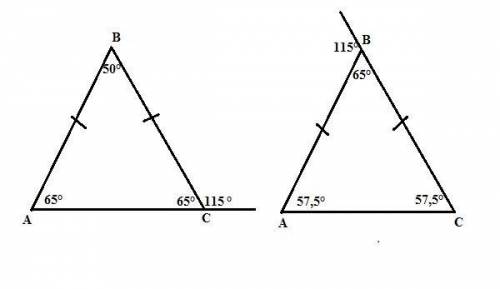
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
1. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
периметр треуг. образованного средними линиями в 2 раза меньше периметра основного треуг. Значит периметр основного треуг. = 60 см.
4 + 5 + 6 = 15
60 / 15 = 4
Таким образом стороны основного треугольника 16, 20, 24
А образованного средними линиями 8, 10, 12.
2. Треугольники MNK и ANB подобны по 2 сторонам и углу между ними, а так как медианы в месте пересечения делятся в соотношении 2 / 1 т.е. от вершины 2 / 3 и 1 / 3, то и сторона MK = AB / 2 * 3 = 12 / 2 *3 = 18 см
3. По теореме Пифагора KP = корень (PT^2 + TK^2) = корень (49*3 + 49) = 14 см
тангенс угла K = PT / TK = 7* корень (3) / 7 = корень (3)
угол K = арктангенс (корень (3)) = 60 градусов.
4. Так как BH высота получаем 2 прямоугольных треугольника AHB и CHB, зная один из катетов и противолежащий ему угол находим две составляющих AC.
АН = BH / тангенс ( угла A), HC = BH / тангенс ( угла С )
АС=AH+HC = 4 / тангенс (альфа ) + 4 / тангенс (бета)
5. так как по определению трапеции верхнее и нижнее основания параллельны т.е. NK параллельна MP и EK = KP из условия, то NK является средней линией треугольника MEP. Следовательно MP = 2 * NK = 14 см.
Разность оснований трапеции = 14 - 7 = 7 см.