6
AD=25
AB=15
BAC=DAC
DB и АВ перпендиккулярны
Накрест лежащие углы CAD и АСВ равны. Тогда АВС равнобедренный и ВС=15
Треугольники ABH и ABD подобны. Отношение:
АВ:АН=АD:АВ
15:АН=25:15
АН=9
Остается найти ВН по теореме Пифагора:
ВН=корень(15^2-9^2)=12
S=(15+25)/2*12=240
ответ: 240
7
Теорема косинусов для треугольника AМC
AC^2=AM^2+MC^2-2*AM*CM*cosAMC
Теорема косинусов для треугольника BМC
BC^2=BM^2+MC^2-2*BM*CM*cosBMC
AC=BC (треугольник равносторонний) Тогда AC^2=BC^2
AM^2+MC^2-2*AM*CM*cosAMC=BM^2+MC^2-2*BM*CM*cosBMC
AM^2-2*AM*CM*cosAMC=BM^2-2*BM*CM*cosBMC
АМ и ВM знаем
2^2-2*2*CM*cosAMC=10^2-2*10*CM*cosBMC
4-4*CM*cosAMC=100-20*CM*cosBMC
Углы ВМС и ВАС равны, опираются на одну дугу. ВАС=60 - равносторонний треугольник.
Угол АМС=АМВ+ВМС=АСВ+ВАС=60+60=120
4-4*CM*cos120=100-20*CM*cos60
4-4*CM*(-1/2)=100-20*CM*1/2
4+2*CM=100-10*CM
12*CM=96
СМ=8
ответ: 8
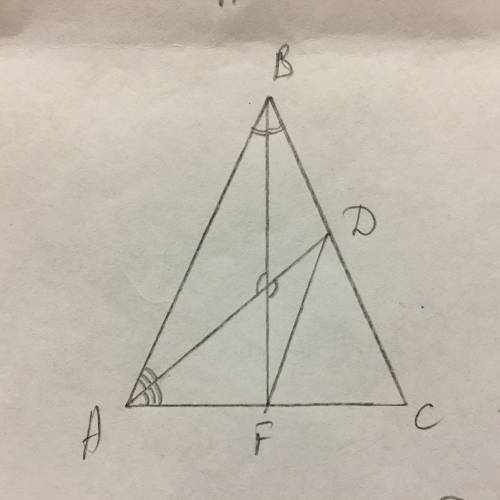
периметр= 2 * боковая сторона + основание
16= 2 * боковая сторона + 6
боковая сторона = (16-6)/2=5
сторона1 = 5
сторона2=5
основание = 6