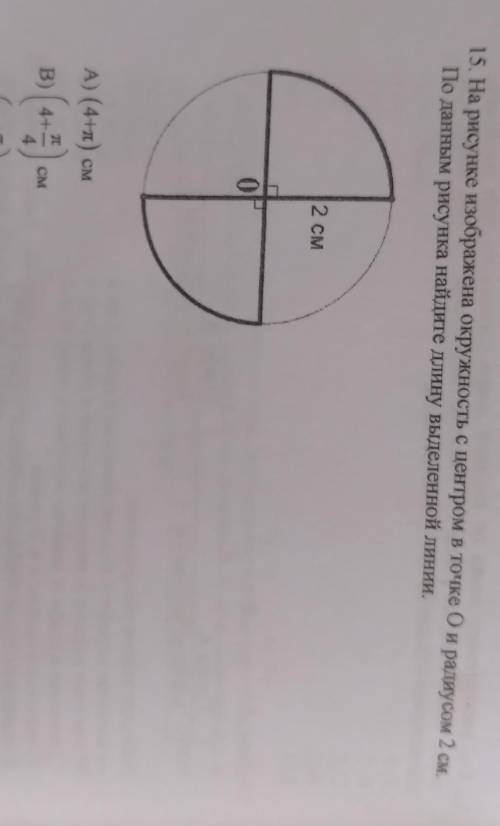
Написала на картинке.
1. Каждая сторона треугольника меньше суммы двух других сторон. Пользуясь этой теоремой, пишем неравенства для сторон шестиугольника.
2. Неравенство для второго вопроса -
PK+KL+LM+MN+NR+PR < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR.
3. Неравенство для третьего вопроса -
2*(PK+KL+LM+MN+NR+PR) < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR+(PK+KL+LM+MN+NR+PR).
4. На картинке.
5. Пользуемся ответами от 3 и 4 задания. Сумма периметров треугольников АВС и DEF равна 12 см (7 см+5 см). Я не знаю, там нужно писать единицы измерения или нет.
Вот такое неравенство в итоге получилось -
2*(PK+KL+LM+MN+NR+PR) < 12 см.
6. Логично, что поделить на 2.
Получаем, что -
2*(PK+KL+LM+MN+NR+PR) < 12 см
PK+KL+LM+MN+NR+PR < 6 см.
Это нам и нужно было доказать.



(1). Рассмотрим треугольник АВD и АСD. У них :
1) АВ=ВС (по условию )
углы 1 и 2 равны (по условию )
сторона AD общая
Из этого следует, что треугольники равны по 1 признаку равенства треугольников.
2) Из равенства треугольников следует равенство соответственных элементов :
1 углы ACD и АВD равны
2 углы АDВ и АDC равны
Следовательно угол АВD = 38 °, a угол ADB = 102°
(2). Углы ENM и KNF в треугольниках вертикальные, из этого следует, что они равны. MN=NK, EN=NF, из этого следует, что треугольники MNE и KNF равны по первому признаку равенства треугольников.
MK = MN + NK, а так как MN=NK, то MN = 1\2MK = 10\2 = 5 см.
Треугольники равны, значит ME = KF = 8 см.