480см³
Объяснение:
Дано:
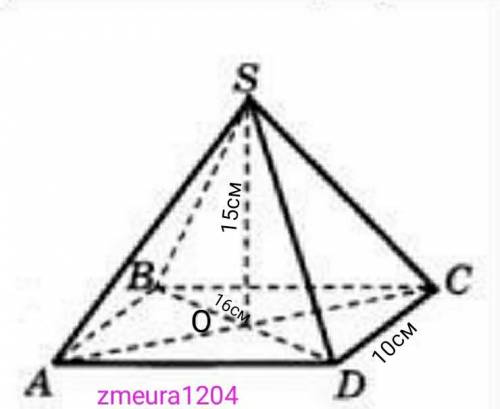
SABCD- пирамида
ABCD- ромб
ВD=16см
АВ=ВС=СD=AD=10см
V=?
Решение
Диагонали ромба пересекаются перпендикулярно и точкой пересечения делятся пополам.
ВО=BD:2=16:2=8см.
∆АВО- прямоугольный треугольник.
По теореме Пифагора
АО=√(АВ²-ВО²)=√(10²-8²)=6см
АС=2*АО=2*6=12см
S(ABCD)=1/2*AC*BD=1/2*16*12=96см² площадь основания.
V=1/3*S(ABCD)*SO=1/3*96*15=480см³
Пункт В) тупоугольный треуголь
ник.
Объяснение:
В треугольнике выполняется
соотношение: против больше
го угла лежит большая сторо
на.
Сначала проверяю теорему
Пифагора. В прямоугоьном
треугольнике большей сто
роной является гипотенуза.
18^2=6^2+13^2
324=36+169
324>205
Так как условие теоремы не
выполняется, значит, треуголь
ник не прямоугольный. То есть
против большей стороны нахо
дится угол, превосходящий пря
мой. Чтобы убедиться, что треу
гольник тупоугольный, исполь
зуем теорему косинусов.
18^2=6^2+13^2-2×6×13cosa
156cosa=36+169-324
156cosa=-119
cosa=-119/156<0
cosa<0
Угол "а" - тупой.
Треугольник тупоугольный.
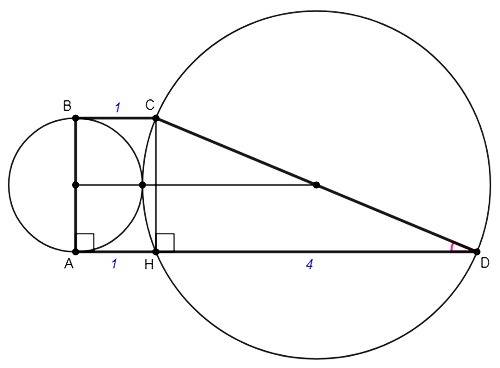
Точка касания двух окружностей лежит на линии их центров. Поскольку центрами являются середины боковых сторон, линией центров является средняя линия трапеции и она равна сумме радиусов или полусумме боковых сторон. А так как средняя линия трапеции равна полусумме оснований, сумма боковых сторон равна сумме оснований.
BC=x, AD=5x
AB+CD=AD+BC=6x
CH - высота, CH=AB
HD=AD-BC=4x
CH+CD=6x <=> CH=6x-CD
CH^2 + HD^2 = CD^2 <=>
(6x-CD)^2 + (4x)^2 = CD^2 <=>
36x^2 -12xCD +CD^2 +16x^2 = CD^2 <=>
CD= 52/12 *x =13/3 *x
cos(D) =HD/CD =4*3/13 =12/13
∠D= arccos(12/13) =22,62°
Об'єм піраміди обчислюється за формулою: \mathrm{V=\frac{1}{3} S_{oc_H}\cdot h}V=
3
1
S
oc
H
⋅h
де Sосн - площа основи; h - висота піраміди.
Основою піраміди є ромб ABCD, діагоналі якого дорівнюють 10 см і 18 см. Тоді площа ромба: \mathrm{S_{ocH}=\dfrac{BD\cdot AC}{2}=\dfrac{18\cdot10}{2}=90}S
ooc = 2
BD⋅AC= 2
18⋅10=90 см²
Об'єм піраміди: \mathrm{V=\frac{1}{3} \cdot90\cdot20=600}V=
31⋅90⋅20=600 см³
ответ: : 600 cм³.