2114 кв.см
Объяснение:
Пирамида в Лувре представляет собой правильную четырёхугольную пирамиду (прототип пирамиды Хеопса)
Правильная четырехугольная пирамида — это многогранник, у которого одна грань — основание пирамиды — квадрат, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр пересечения диагоналей квадрата основания из вершины.В основании пирамиды находится квадрат площадью 1225 кв.м. Значит сторона квадрата равна:
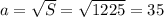
Высота пирамиды- SO=21,6
Для нахождения полной площади поверхности пирамиды нужно сложить площадь боковой поверхности и площадь основания.Sполн. = Sбок. + Sосн.
Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему:Sбок=p×l
р=Р/2=4а/2=2а=2×35=70 см
Апофему SF найдём из прямоугольного треугольника SFO(<O=90°) по теореме Пифагора.
SO=21,6 - по условию. ОF= 1/2×AB=1/2×35=17,5 см
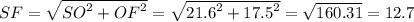
Sбок=70×12,7=889 кв.см
Sполн= 889+1225=2114 кв.см
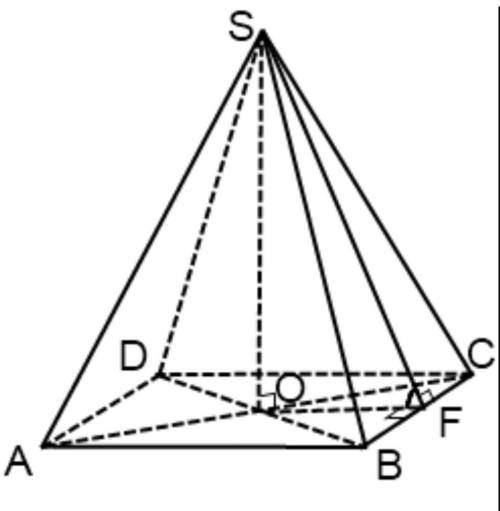
ВД=3√2см
Объяснение:
У равнобедренных прямоугольных треугольников острые углы равны по 45°, поэтому ∠ВАС=∠ВСА=∠САД=∠АСД=45°. У треугольников АВС и АВД острые углы по 45° и общая гипотенуза АС=6см, значит треугольники равны по 4-му признаку – гипотенузе и острому углу, тогда АВ=ВС=АД=СД. При этом АС является основанием в обоих треугольниках. Проведём высоты ВК и ДК к гипотенузе АС. Так как треугольники равнобедренные, то высота, опущенная к основанию является ещё биссектрисой и медианой. Так как треугольники равны, то их медианы также будут равны. Медиана прямоугольного треугольника, проведённая из вершины прямого угла к гипотенузе равна её половине, тогда ВК=ДК=АС÷2=6÷2=3см.
∆ВДК – прямоугольный, (по условию, так как плоскости треугольников перпендикулярны), где ВК и ДК – катеты, а ВД – гипотенуза. Найдём ВД по теореме Пифагора:
ВД²=ВК²+ДК²=3²+3²=9+9=18
ВД=√18=3√2см.
Можно найти другим . В равнобедренном прямоугольном треугольнике гипотенуза больше катета в √2 раз, тогда ВД=3√2см
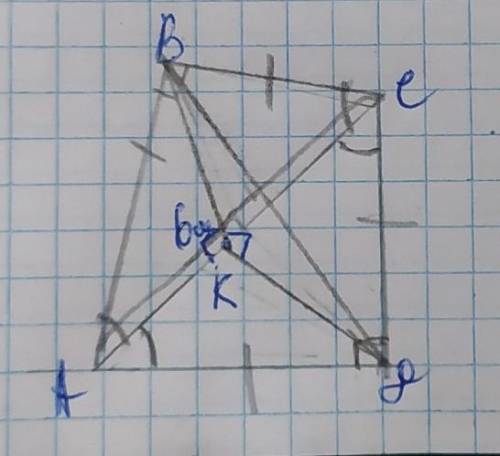
Объяснение:
Надеюсь , удачи, если не правильно Прости !!