5
Объяснение:
Гипотенуза 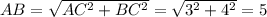 . Радиус вписанной в прямоугольный треугольник окружности
. Радиус вписанной в прямоугольный треугольник окружности 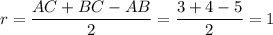 . Площадь
. Площадь 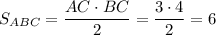 .
.
Рассмотрим четырёхугольник OA₁CB₁: ∠С = 90° по условию, ∠A₁ = ∠B₁ = 90° как углы между радиусом и касательной, тогда ∠O = 360° - ∠C - ∠A₁ - ∠B₁ = 360° - 3·90° = 90°. Значит, OA₁CB₁ — прямоугольник, но поскольку OA₁ = OB₁ = r, это квадрат. Тогда OA₁ = OB₁ = B₁C = A₁C = 1.
AC₁ = AB₁ как отрезки касательных, проведённых из одной точки. При этом AB₁ = AC - B₁C = 4 - 1 = 3, т. е. AC₁ = AB₁ = 3. Аналогично BC₁ = A₁B = BC - A₁C = 3 - 1 = 2.
Найдём площадь 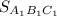 путём вычитания площадей
путём вычитания площадей 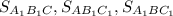 из площади
из площади 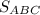 :
:
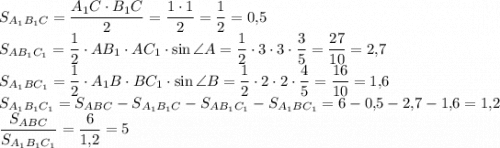
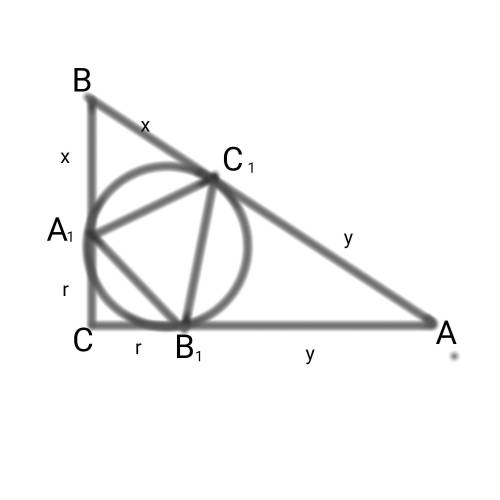
Площадь круга, как Вы помните, находят по формуле
S=πr²
Радиус находим из остроугольных треугольников, образовавшимися диагоналями при меньшей стороне прямоугольника.
Эти треугольники - равносторонние, т.к. угол при пересечении диагоналей равен 60°, а сами диагонали делятся пополам и этим образуют равнобедренные треугольники, углы которых при основании, равном меньшей стороне вписанного прямоугольника, тоже равны 60°.⇒cледовательно, каждая половина диагонали равна меньшей стороне прямоугольника. А так как диагонали здесь являются диаметрами окружности, то радиус описанного круга тоже равен меньшей стороне прямоугольника.
r=10 см
S=πr²,
S=100 π см²