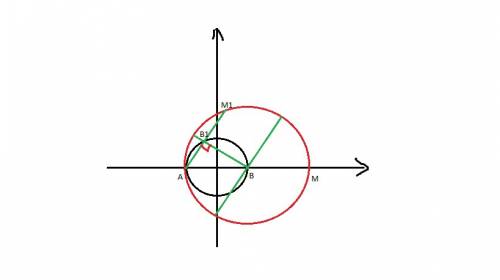
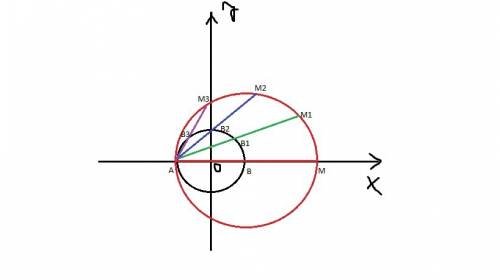
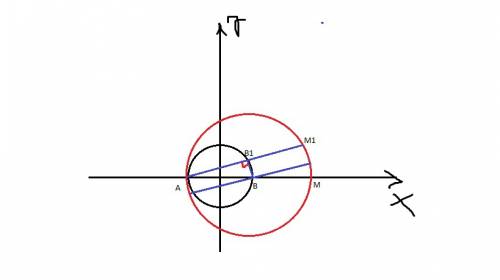
Постройте окружность радиуса 2 см с центром в точке О и касательную A. Отложите на касательной точку M, на расстоянии 3 см от точки касания А. Проведите из точки М касательную b к данной окружности, не совпадающую с A Точку касания обозначьте В. Найдите длину отрезка сор
Докажем второй пункт. Как известно, высота равнобедренного треугольника совпадает с его медианой и биссектрисой и является его осью симметрии. Также, любые два равнобедренных треугольника, построенные на одном основании, обладают общей осью симметрии и, как следствие, общей высотой/медианой/биссектрисой. Тогда получаем, что KA⊂KC и все три точки лежат на KC.
Это автоматически доказывает первый пункт, т.к. непонятные ∠ACB и ∠ACD превращаются в углы при биссектрисе ∠KCB=∠KCD, которые равны между собой.