Объяснение:
радиус сферы описанного около конуса равен радиусу конуса. так как центр основания конуса и центр сферы совпадают Rc=rк
радиус сферы описанного около конуса равен высоте конуса Rс=rк=Hк.
высота конуса перпендикулярно к основанию конуса.
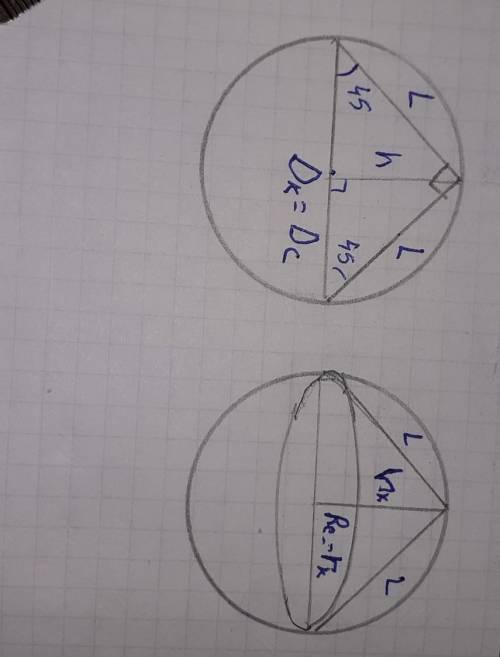
при осевом сечении конуса выходит фигура равнобедренный прямоугольный треугольник.
где образующая L конуса катеты, а основание гипотенуза равное диаметру Dк конуса. По теореме Пифагора. а²+в²=с²
находим гипотенузу равную диаметру D=2R
Dк=√L²+L²
Dк=√(7√2)²+(7√2)²=√49×2+49×2=√98+98=√196=14
Dк=Dс=14
радиус сферы
Rc=Dc/2=14/2=7
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
Объяснение:
Рисунок прилагается.
Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.
Найти катеты AC и BC.
Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.
Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.
h² = a₁*b₁ = 2 * 18 = 36; h = 6
⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.
Из прямоугольного ΔACH по теореме Пифагора:
a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10
Катет AC = 2√10 см/
Из прямоугольного ΔBCH по теореме Пифагора:
b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10
Катет BC = 6√10 см.
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

В какой фигуре,как построены углы,вершины,что против чего лежит.
1.Это не может быть треугольник,ведь вершин 4 - ABCD.
2.Если это трапеция,,параллелограмм,или другая фигура с 4 углами,то
все зависит от того какая фигура и где стоят вершины.
3.Если это окружность,и есть диаметр,то
∠DAB = ∠DCA + ∠ACD.
∠ACD = 41°
∠ACB = 90° (как вписанный угол, опирающийся на диаметр окружности).
∠DAB = 41° + 90° = 131°.