Дано:
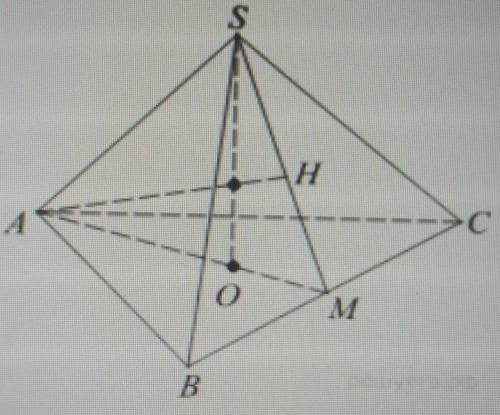
SABC - правильная треугольная пирамида
SO - высота SO⊥(ABC)
AB = BC = AC = √10
SA = SB = 5
-------------------------------------------------------------------
Найти:
р(AS, BC) - ?
ΔABC - равносторонний, поэтому:
AO = AB/√3 = √10/√3 × √3/√3 = √30/3
SA² = SO² + AO² ⇒ SO = √SA² - AO² - теорема Пифагора
SO = √5² - (√30/3)² = √25 - 30/9 = √225-30/9 = √195/9 = √195/3
Теперь мы находим объем Пирамиды:
V = 1/3 × Sосн × SO = 1/3 × AB²√3/4 × SO = 1/3 ×(√10)²×√3/4 × √195/3 = 1/3 × 10√3/4 × √195/3 = 1/3 × 5√3/2 × √195/3 = 5√585/18 = 5×√9×65/18 = 5×3√65/18 = 15√65/18 = 5√65/6
Но с другой стороны можно и так записать формулу:
V = 1/3 × S(ΔBCS) × h (1), где h – искомое расстояние ⇒ р(AS, BC) = h
Проведем SM⊥BC ⇒ SM = h.
Так как ΔSMB - прямоугольный (∠SMB = 90°), тогда используется по теореме Пифагора:
SB² = SM² + MB² ⇒ SM = √SB² - MB² - теорема Пифагора
MB = BC/2 = √10/2
SM = √5² - (√10/2)² = √25 - 10/4 = √100-10/4 = √90/4 = √90/2 = √9×10/2 = 3√10/2
И теперь находим площадь ΔSBC:
S(ΔSBC) = 1/2 × SM × BC = 1/2 × 3√10/2 × √10 = 30/4 = 15/2
И теперь мы находим высоту из объема пирамиды (1):
V = 1/3 × S(ΔBCS) × h ⇒ h = 3V/S(ΔBCS) - нахождение высоты ΔSBC
h = 3 × 5√65/6 / 15/2 = 5√65/2 / 15/2 = 5√65/12 = √65/3 ⇒ SM = р(AS, BC) = h = √65/3
ответ: р(AS, BC) = √65/3
P.S. Рисунок показан внизу↓
1) АВ=ВС=7,04дм АС=4,04дм
2)ЕМ=MF=10, EF=15
3) АС=3м, АВ=ВС=2,4м
Объяснение:
1) Треугольник АВС равнобедренный, т.к. АВ=ВС
представляем АС=АВ-3дм
Р=АВ+ВС+АС=2АВ+(АВ-3дм)=2АВ+АВ-3дм=3АВ-3дм
АВ=(Р+3дм)/3=(18,12+3)/3=7,04дм
АС=7,04-3=4,04 дм
2)Треугольник равнобедренный т.к. ЕМ=МF, представляем сторону, как
EF=(3*ЕМ)/2
как в задаче выше P=2*ЕМ+EF=2ЕМ+(3*ЕМ)/2=(4ЕМ+3ЕМ)/2=7/2ЕМ
ЕМ=MF=(Р*2)/7=35*2/7=10
EF=10*3/2=15
3) так угол А=углу С, то треугольник АВС равнобедренный, значит
АВ=ВС=0,8АС
Р=2*0,8АС+АС=1,6АС+АС=2,6АС
АС=Р/2,6=7,8/2,6=3м
АВ=ВС=3*0,8=2,4м