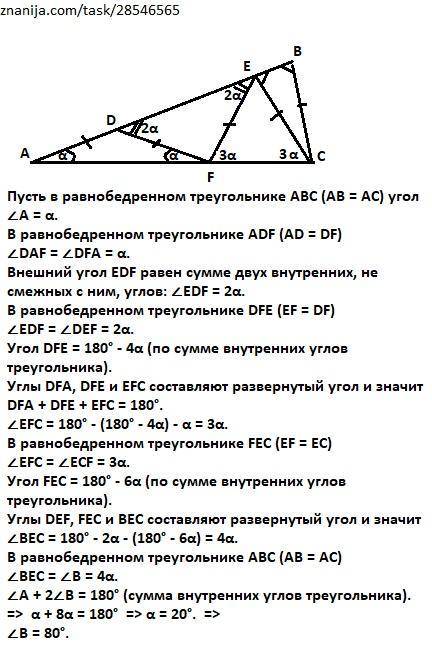
∠АВС = 80°.
Объяснение:
Пусть в равнобедренном треугольнике АВС (АВ = АС) угол
∠А = α.
В равнобедренном треугольнике ADF (AD = DF)
∠DAF = ∠DFA = α.
Внешний угол EDF равен сумме двух внутренних, не смежных с ним, углов: ∠EDF = 2α.
В равнобедренном треугольнике DFЕ (EF = DF)
∠EDF = ∠DEF = 2α.
Угол DFE = 180° - 4α (по сумме внутренних углов треугольника).
Углы DFA, DFE и EFС составляют развернутый угол и значит
DFA + DFE + EFС = 180°.
∠EFC = 180° - (180° - 4α) - α = 3α.
В равнобедренном треугольнике FЕС (EF = ЕС)
∠EFС = ∠EСF = 3α.
Угол FEС = 180° - 6α (по сумме внутренних углов треугольника).
Углы DЕF, FEC и BEC составляют развернутый угол и значит
∠ВЕС = 180° - 2α - (180° - 6α) = 4α.
В равнобедренном треугольнике АВС (АВ = АС)
∠ВЕС = ∠В = 4α.
∠А + 2∠В = 180° (сумма внутренних углов треугольника). => α + 8α = 180° => α = 20°. =>
∠В = 80°.
Кут АОС=ВОМ, бо вони вертикальні, а вертикальні кути рівні між собою.
Кут АОМ=СОВ, бо вони вертикальні, а вертикальні кути рівні між собою.
Нехай ∠СОВ+∠ВОМ+∠АОМ=286°.
Суміжними називаються два кути, у яких одна сторона спільна, а дві інші є продовженням одна одної.
Сума суміжних кутів дорівнює 180°.
∠СОВ+∠ВОМ=180°, бо вони суміжні.
∠АОМ+∠АОС=180°, бо вони суміжні.
Виходить, що сума всіх кутів, що утворилися в результаті перетину прямих дорівнює 360°:
∠СОВ+∠ВОМ+∠АОМ+∠АОС=180°+180°
∠СОВ+∠ВОМ+∠АОМ+∠АОС=360°
Оскільки ∠СОВ+∠ВОМ+∠АОМ=286°, виходить
286°+∠АОС = 360°
∠АОС=360-286
∠АОС=74°.
Виходить, що ∠АОС=∠ВОМ=74°.
Тепер оскільки ∠СОВ+∠ВОМ=180°, то
∠СОВ+74°=180°
∠СОВ=180°-74°
∠СОВ=106°.
Виходить, що ∠СОВ=∠АОМ=106°.
Відповідь: два кути по 74° та два кути по 106°.