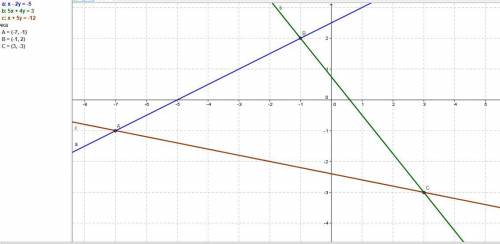
Даны уравнения прямых, проходящих через стороны треугольника ABC:
AB : x – 2y + 5 = 0
BC : 5x + 4y – 3 = 0
AC : x + 5y + 12 = 0.
Пересечение прямых АВ и ВС (точка В - общая) даёт точку В.
AB : x – 2y + 5 = 0 х2 = 2x - 4y + 10 = 0
BC : 5x + 4y – 3 = 0 5x + 4y - 3 = 0
7x + 7 = 0, x = -7/7 = -1, y = (x + 5)/2 = 2.
Точка В(-1; 2).
Аналогично определяем точку А.
AC : x + 5y + 12 = 0.
AB : x – 2y + 5 = 0 вычитаем
7y + 7 = 0, y = -7/7 = -1, x = 2y - 5 = -7.
Точка А(-7; -1).
Определяем точку С.
BC : 5x + 4y – 3 = 0 5x + 4y - 3 = 0
AC : x + 5y + 12 = 0. х(-5) = -5x - 25y - 60 = 0
-21y - 63 = 0. y = -63/21 = -3, x = -5x - 12 = 3.
Точка С(3; -3).
<2=<5=143 градуса,как вертикальные
<3=<2=143 градуса,как накрест лежащие
<8=<3=143 градуса,как вертикальные
<2+<4=180 градусов,как односторонние
<4=180-143=37 градусов
<1=<4=37 градусов,как накрест лежащие
<6=<1=37 градусов,как соответственные
<7=<6=37 градусов,как внешние накрест лежащие
Номер 2
<1=<4=48 градусов,как накрест лежащие
<3+<1=180 градусов,как односторонние
<3=180-48=132 градуса
<7=<1=48 градусов,как вертикальные
<6=<4=48 градусов,как вертикальные
<5=<3=132 градуса,как соответственные
<8=<5=132 градуса,как внешние накрест лежащие
<2=<8=132 градуса,как соответственные
Объяснение: