DOA = 70°. Дано в задаче.
BOC = DOA = 70°. Вертикальные углы равны (1).
DOC = 180° - 70° - 110°. Смежные углы в сумме дают 180° (2).
AOB = DOC = 110°. (1).
ODC = (180° - 110°) / 2 = 35°. Сумма углов треугольника равна 180° (3). Если треугольник равнобедренный, то углы при его основаниях равны (4).
ADO = 90° - 35° = 55°. Два угла составляют прямой угол (5).
OAD = ADO = 55°. (4).
OAB = 90° - 55° = 35°. (5).
OBA = OAB = 35°. (4).
OBC = 90° - 35° = 55°. (5).
OCB = OBC = 55°. (4).
Все остальные углы состоят из других и их можно посчитать по сумме. Например:
DAB = DAO + BAO = 55° + 35° = 90°.
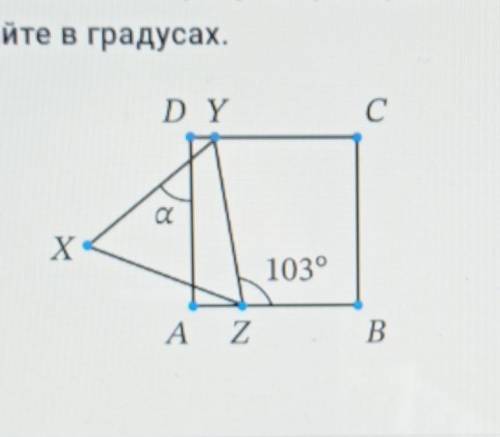
1.Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Решение.
Треугольники HOBи KOB равны, т. к. являются прямоугольными с общей гипотенузой и равными катетами, значит, HB=KB=3
PABC=AC+CB+AH+HB=2CB+2HB=16+6=22
ответ: 22
2. В равнобедренный треугольник АВС с основанием ВС вписана окружность. Она касается стороны АВ в точке М. Найдите радиус окружности, если АМ = 8 и ВМ = 12.
S=1/2p*r
r=2s/p
Т.к треугольник ABC-равнобедренный, то AB=AC=30
По свойству касательных: АМ=АЕ=8, СЕ=СК=12,ВМ=КВ=12,значит ВС=24
По формуле Герона S треугольник = в корне p(p-a)(p-b)(p-c)
47
Объяснение:
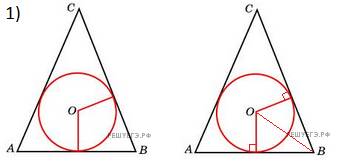
Так как XYZ равносторонний треугольник, то его все углы равны по 60 градусов. => угол XZB = 103 + 60 = 163 градуса. Угол XZA = 180 - 163 = 17 градусов.
Не могу обозначит, т.к. на рисунке не установлена точка, но маленький треугольник внизу является прямоугольным, т.к. один из его углов является углом квадрата, который равняется, разумеется, 90 градусов. А значит, верхний угол этого треугольника будет равен 180-(90+17) = 73 градуса. Его вертикальный угол будет равен тоже 73 градуса по свойству вертикальных углов. Опять же, поскольку треугольник XYZ - равносторонний, то его угол ZXY равен 60 градусов.
Находим угол а. а = 180 - (60 + 73) = 47 градусов.