Решение можно найти двумя
Решение можно найти двумя Проекция боковой грани на основание для правильного тетраэдра равна 1/3 площади основания:
Решение можно найти двумя Проекция боковой грани на основание для правильного тетраэдра равна 1/3 площади основания:So(б.гр) = (1/3)So = 1/3)(a²√3/4) = (a²√3/12) = (8²√3)/12 = (64√3)/12 =
Решение можно найти двумя Проекция боковой грани на основание для правильного тетраэдра равна 1/3 площади основания:So(б.гр) = (1/3)So = 1/3)(a²√3/4) = (a²√3/12) = (8²√3)/12 = (64√3)/12 == 16√3/3 см².
Решение можно найти двумя Проекция боковой грани на основание для правильного тетраэдра равна 1/3 площади основания:So(б.гр) = (1/3)So = 1/3)(a²√3/4) = (a²√3/12) = (8²√3)/12 = (64√3)/12 == 16√3/3 см².2) Для правильного тетраэдра высота основания h равна апофеме A боковой грани. Проекция апофемы на основание равна (1/3) высоты основания.
Решение можно найти двумя Проекция боковой грани на основание для правильного тетраэдра равна 1/3 площади основания:So(б.гр) = (1/3)So = 1/3)(a²√3/4) = (a²√3/12) = (8²√3)/12 = (64√3)/12 == 16√3/3 см².2) Для правильного тетраэдра высота основания h равна апофеме A боковой грани. Проекция апофемы на основание равна (1/3) высоты основания.Косинус угла α наклона боковой грани равен (1/3)h)/(1A) = 1/3.
Решение можно найти двумя Проекция боковой грани на основание для правильного тетраэдра равна 1/3 площади основания:So(б.гр) = (1/3)So = 1/3)(a²√3/4) = (a²√3/12) = (8²√3)/12 = (64√3)/12 == 16√3/3 см².2) Для правильного тетраэдра высота основания h равна апофеме A боковой грани. Проекция апофемы на основание равна (1/3) высоты основания.Косинус угла α наклона боковой грани равен (1/3)h)/(1A) = 1/3.Площадь проекции боковой грани на основание равна:
Решение можно найти двумя Проекция боковой грани на основание для правильного тетраэдра равна 1/3 площади основания:So(б.гр) = (1/3)So = 1/3)(a²√3/4) = (a²√3/12) = (8²√3)/12 = (64√3)/12 == 16√3/3 см².2) Для правильного тетраэдра высота основания h равна апофеме A боковой грани. Проекция апофемы на основание равна (1/3) высоты основания.Косинус угла α наклона боковой грани равен (1/3)h)/(1A) = 1/3.Площадь проекции боковой грани на основание равна:So(б.гр) = S(б.гр)*cos α = (8²√3/4)*(1/3) = (64√3)/12 = 16√3/3 см².
Объяснение:
как то так
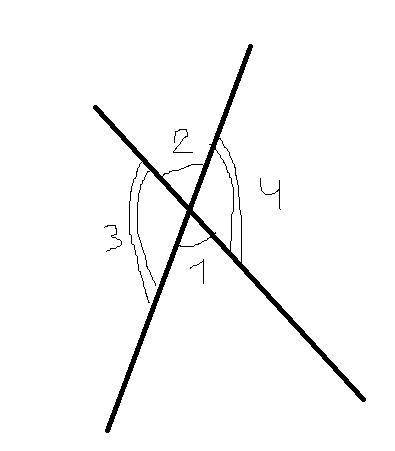
При пересечении двух прямых образуются только углы двух видов: смежные и вертикальные.
Перпендикулярные прямые рассматривать смысла нет: все углы по 90° и условие не выполняется, поэтому есть 2 тупых и 2 острых угла.
У смежных углов сумма равна 180°.
То есть даже на примере:
∠1 смежен с ∠3 и ∠4, то есть ∠1+∠3=180°, ∠1+∠4=180°
Аналогично ∠2 смежен с теми же углами. И ∠1=∠2.
И это явно не могут быть 2 тупых угла, так как они как вертикальные равны между собой, но если ∠3+∠4=140° и ∠3=∠4, то ∠3=∠4=70°, а они тупые, то есть такого быть не может. Поэтому это могут быть только ∠1 и ∠2, которые равны по 70° и являются друг для друга вертикальными.
Что и требовалось доказать.
30
Объяснение:
окружность вписанная в треугольник касается его в центре сторон треугольника тогда стороны треугольника равны 8 , 10 и 12 и периметр равен 30