В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. Доказательство.Обратимся к рисунку, на котором АВС — равнобедренный треугольник с основанием ВС, АD — его биссектриса.Из равенства треугольников АВD и АСD (по 2 признаку равенства треугольников:AD-общая;углы 1 и 2 равны т.к. AD-биссектриса;AB=AC,т.к. треугольник равнобедренный) следует, что ВD = DC и 3 = 4. Равенство ВD = DC означает, что точка D — середина стороны ВС и поэтому АD — медиана треугольника АВС. Так как углы 3 и 4 смежные и равны друг другу, то они прямые. Следовательно, отрезок АО является также высотой треугольника АВС. Теорема доказана. В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой Если в треугольнике два угла равны, то он равнобедренный. Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.
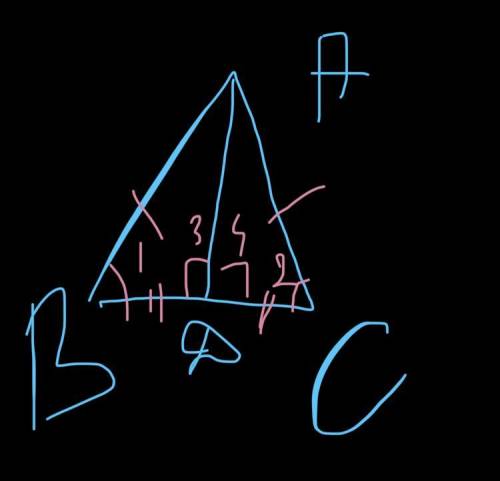
Центр вписаного кола лежить на перетині бісектрис трикутника АВС. Тоді у трикутнику АОС АО=ОС як радіуси. Маємо трикутник АОС-рівнобедрений.Якщо кут при вершині О цього трикутника = 100 градусів (АОС), то кути при основі рівнобедреного трикутника рівні, та дорівнюють (180-100)/2=40 градусів.
АО та СО є бісектриса и кутів САВ та ВСА трикутника АВС. Тоді ці кути будуть рівні 40*2=80 градусів. Кут АВС трикутника АВС тоді дорівнює 180-(80+80)=20 градусів.