У тетраэдра все ребра равны. Так как по условию, точки М, К, Р середины отрезков АВ, ВД, ВС, то отрезок КМ средняя линия треугольника АВД, КР – средняя линия треугольника ВСД, МР – средняя линия треугольника АВС.
Отрезки средних линий параллельны основаниям треугольников: MK || АД, КР || СД, МР || АС, тогда и плоскость МКР параллельны плоскости АСД, что и требовалось доказать.
Длина средней линии треугольника равна половине длины параллельной стороны, тогда треугольник МКР подобен треугольнику АСД по трем пропорциональным сторонам с коэффициентом подобия К = АД / МК = АД / (АД / 2) = 2.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Sавс / Sмкр = 48 / Sмкр = 22.
Sмкр = 48 / 4 = 12 см2.
ответ: Площадь треугольника МКР равна 12 см2.
Объяснение: правильно? ;-;
В прямоугольном треугольнике найти все линейные элементы
Объяснение:
ΔKNT подобен ΔMKT по 2-м углам: ∠МТК=NTK=90, ∠M=∠TKN.
Значит сходственные стороны пропорциональны :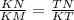 
.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой ⇒ КТ=√( МТ*ТN) .
, 
, 
, 
.
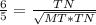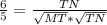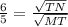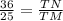Из условия TN=11+MT , поэтому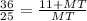 
, 36MT=25(11+MT) , MT=25. Тогда TN=11+25=36 , гипотенуза MN=25+61=61.
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и проекций катетов на гипотенузу :
а) катет МК=√(МN*MT) , MK=√(25*61)=5√61;
б) катет КN=√(МN*TN) , KN=√(36*61)=6√61.
в) высота КТ=√( МТ*ТN) , КТ=√( 25*36)=30 .
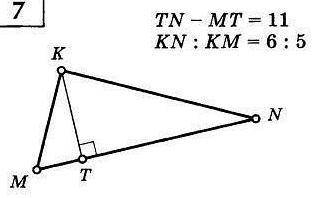
Решение задания прилагаю