QS=54
Объяснение:
Новое решение.
Исходя из суммы углов треугольника, в треугольнике RPQ угол при верщине R = 30 градусам. Что означает, что в прямоугольном треугольнике RPQ катет равен половине гипотенузы, то есть RP=2*PS=36.
Аналогично в треугольнике RPQ угол Q=30 градусов, а значит гипотенуза PQ=2*RP=72.
Следовательно QS=PQ-PS=72-18=54
Старое решение:
Исходя из суммы углов треугольника, угол при верщине Q = 30 градусам. Тогда из треугольника tg60=RS/PS, а tg30=RS/QS
RS=tg60*PS
RS=tg30*QS
tg60*PS=tg30*QS -> QS=(tg60*PS)/tg30=tg60*ctg30*PS
т.к. tg a * ctg b =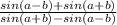 
тогда Q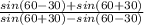S=
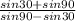*PS=
*PS=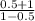
*PS=(1.5/0.5)*PS=3*PS
QS=3*18=54
Объяснение:
Перпендикулярные прямые — две прямые, которые пересекаются под прямым углом.
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.
Перпендикуляр к данной прямой — отрезок прямой, перпендикулярной данной прямой, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называют основанием перпендикуляра.
Существование и единственность перпендикулярной прямой.
Через каждую точку прямой можно провести перпендикулярную ей прямую, причем только одну.
Через каждую точку вне данной прямой можно провести перпендикулярную к ней прямую и к тому же только одну.
АВ=х, ВС=420/х
АС в квадрате = АВ вквадрате + ВС в квадрате
841 = х в квадрате + 176400 / х в квадрате
х (4) -841 х в квадрате +176400=0 (4) - степень
х в квадрате = (841+- корень (707281 - 4*176400)) / 2
х в квадрате =(841+-41) / 2
х1 в квадрате =400, х1=20=АВ=СД
х2 в квадрате =441, х2=21=ВС=АД
периметр=20+20+21+21=82