Площадь боковой поверхности правильной усечённой пирамиды равна пололовине произведения суммы периметров её оснований и апофемы (высоты боковой грани).
S=(Р1+Р2)*А/2, где Р1 и Р2 - периметры, А - апофема (высота боковой грани правильной пирамиды)
Р1=4*6=24см - периметр нижнего основания.
Р2=2*6=12см - периметр верхнего основания пирамиды.
Найдем высоту боковой грани правильной пирамиды - апофему.
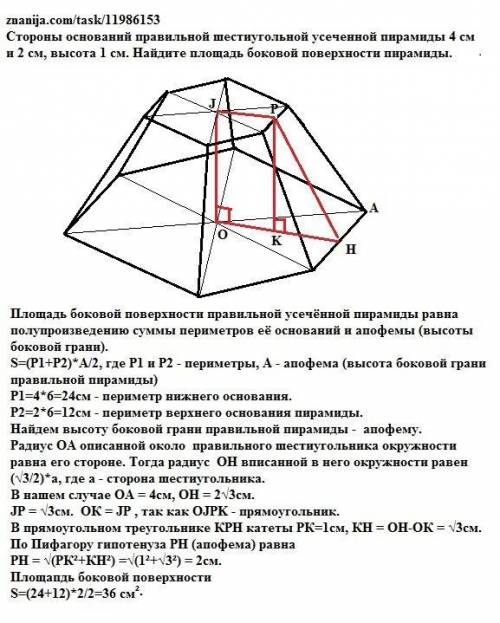
Радиус ОА описанной около правильного шестиугольника окружности равна его стороне. Радиус ОН вписанной в него окружности равен (√3/2)*а, где а - сторона шестиугольника. (по формуле или из прямоугольного треугольника НОР по Пифагору).
В нашем случае ОА = 4см, ОН = 2√3см.
Для верхнего основания JP = √3см.
ОК = JP , так как ОJPK - прямоугольник.
В прямоугольном треугольнике КРН катеты РК=1см,
КН = ОН-ОК = √3см.
По Пифагору гипотенуза PH (апофема) равна
РН = √(РК²+КН²) =√(1²+√3²) = 2см.
Площапдь боковой поверхности
S=(24+12)*2/2=36 см².
АС=4,4см
СВ=10см
Объяснение:
cos<A=AC/AB
0,4=AC/11
AC=11*0,4=4,4 см
Теорема Пифагора.
СВ=√(АВ²-АС²)=√(121-19,36)=√101,64≈10см, округлено до целого числа.