2 ВАРИАНТ 1.В прямоугольнике ABCD точка О является точкой пересечения диагоналей, AC =
8 см, а периметр треугольника AOD равен 19 см. Найдите длину стороны AD.
А) 4
В) 8 C) 9
D) 11

👇

Увидеть ответ

Ответ:

catBoss009

16.01.2021

D) 11

Объяснение:

1. В прямоугольнике диагонали имеют равные длины.

2. В прямоугольнике диагонали пересекаются и в точке пересечения делятся пополам.

▪︎Следовательно:

АО = ОD = AC/2 = 8/2 = 4 (как половинки диагоналей АС и ВD).

Р(△AOD) = АО + ОD + AD

19 = 4 × 2 + AD

AD = 19 - 8

AD = 11

4,7(44 оценок)

Открыть все ответы

Ответ:

andrwy1229

16.01.2021

Все, что курсивом - "теория", нужная для решения. В конце - само решение.
Расстояние между скрещивающимися прямыми в общем случае находится так. Надо найти две параллельные плоскости, каждая из который содержит одну из прямых. Расстояние между этими плоскостями и будет искомым расстоянием.
Плоскость A1DC1 содержит прямую DC1. Треугольник A1DC1 - равносторонний, что означает, что трехмерная фигура D1A1DC1 - правильная треугольная пирамида, и вершина D1 проектируется на основание A1DC1 в центр K правильного треугольника A1DC1, то есть D1K перпендикулярно плоскости A1DC1 (это - высота пирамиды).
Кроме того, фигура BA1DC1 - тоже правильная треугольная пирамида (это - вообще правильный тетраэдр, все его ребра равны), и поэтому BK - высота этого тетраэдра к грани A1DC1, то есть BK перпендикулярно A1DC1.
Через точку K можно провести только одну прямую, перпендикулярную плоскости A1DC1, и на этой прямой лежат точки B и D1.
То есть, доказано, что плоскость A1DC1 перпендикулярна диагонали куба BD1.
Точно также можно доказать, что BD1 перпендикулярно плоскости AB1C, и поэтому плоскости AB1C и A1DC1 параллельны. Но параллельность этих плоскостей и так очевидна, поскольку A1C1 II AC; A1D II B1C; и разумеется, AB1 II DC1; но для доказательства параллельности достаточно указать две пары параллельных прямых. Однако то, что обе эти плоскости перпендикулярны диагонали BD1 - важно.
Если рассмотреть внимательнее тетраэдр BA1DC1, можно заметить, что плоскость AB1C пересекает "боковое ребро" BA1 в середине (диагонали квадрата A1B и AB1 делятся точкой пересечения пополам), поэтому сечение тетраэдра BA1DC1, параллельное грани тетраэдра A1DC1, - это такая "средняя плоскость", то есть она разделит пополам и остальные боковые ребра (BD и BC1, что можно увидеть и так) и, главное - высоту BK (по теореме Фалеса).
Аналогично можно показать, что плоскость A1DC1 делит пополам высоту тетраэдра D1AB1C. Если обозначить K1 - центр треугольника AB1C, то получается D1K1 = KK1 = K1B;
Все это - длинная теория, которую труднее набрать, чем понять.
Поскольку KK1 - отрезок прямой BD1, перпендикулярной обеим плоскостям A1DC1 и AB1C, то это и есть расстояние между этими плоскостями, а заодно - и расстояние между скрещивающимися прямыми DC1 и CB1.
Длина диагонали BD = 2√3, KK1 = 2√3/3;

4,8(39 оценок)

Ответ:

Ekaterina2348

16.01.2021

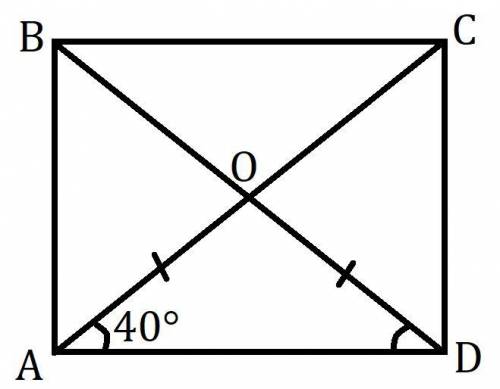
Дан прямоугольник ABCD, ∠CAD:∠CAB=4:5.

Углы прямоугольник равны по 90°.

Пусть ∠CAD=4x, тогда ∠CAB=5x.

∠CAD+∠CAB=∠DAB

4x+5x=9x=90°

x=90°:9=10°

∠CAD=4x=40°

Диагонали в прямоугольнике делятся точкой пересечения пополам.

Пусть AC∩BD=O, тогда AO=DO

В равнобедренном ΔAOD (O-вершина) углы при основании равны. ∠ODA=∠OAD=40°. Сумма углов в треугольнике равна 180°. Откуда ∠AOD=180°-∠ODA-∠OAD=180°-40°-40°=100°

∠AOD>90° ⇒ угол между диагоналями это ∠AOB, смежный с ∠AOD.

∠AOB=180°-∠AOD=180°-100°=80° по свойству смежных углов.

ответ: 80.