α = 45°
Объяснение:
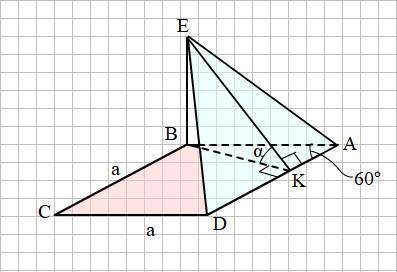
Смотри прикреплённый рисунок.
Из вершины В ромба проводим высоту ВК.
ВК = а · sin A = a · sin 60° = 0.5a√3.
Соединим точку Е с точкой К. ВК является проекцией наклонной ЕК на плоскость АВСD. Поскольку ВК - высота ромба. то ВК ⊥ AD.
По теореме о трёх перпендикулярах: если AD ⊥ BK (проекции наклонной ЕК), то AD⊥ ЕК. Следовательно, ∠ЕКВ = α является линейным углом, служащим мерой двугранного угла между плоскостями ADE и АВСD.
Найдём этот угол.
tg α = BE : BK = 0.5a√3 : 0.5a√3 = 1.
Следовательно, ∠α = 45°
x=8
Объяснение:
а-b+c = (-7-1+x; 4-3+(-5)) = (-8+x; -4)
|a-b+c|=√((-8+x)²+(-4)²) =
=√(64+x²-16x+16) =√(x²-16x+80) = min → будет минимальным, если:
x²-16x+80 = min
это парабола, а=1>0 → минимальное значение будет в вершине параболы:
х(вершины)=-b/2a=-(-16)/(2*1)=16/2=8