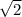 , ∠А=45°
, ∠А=45°Запишем формулу для нахождения радиуса окружности, описанной около правильного многоугольника:
R=a/(2sin×(180°/n)),
где а - длина стороны многоугольника, n – количество сторон правильного многоугольника.
Нам дан шестиугольник, значит n=6.
Найдем угол:
180°:6=30°.
Используя тригонометрическую таблицу, найдем sin(30°):
sin(30°)=1/2.
Перепишем формулу для радиуса описанной окружности:
R=a/(2×1/2)=а/1=а.
Значит, радиус описанной около правильного шестиугольника окружности, стороне шестиугольника:
R=3 см.
ответ: R=3 см.

1. (2 ; -5)
2. (2 ; -4)
3. 3
Объяснение:
1. Уравнение окружности имеет вид (x - а)² + (y - b)² = r², где (а;b) - координаты центра окружности.
2. х =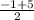 = 2
= 2
у =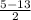 = -4
= -4
3. 2R =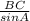 = 3
= 3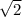 *
* 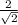 = 6; R = 3
= 6; R = 3