
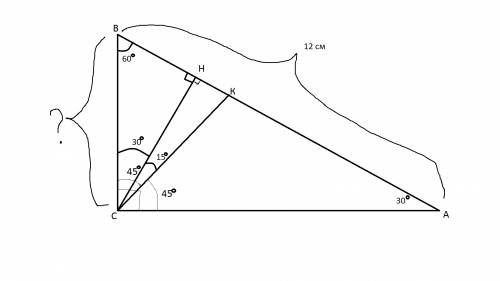
Так как СК - биссектриса угла АСВ, то угол ВСК = углу КСА = 45 градусов.
При этом угол ВСК равен сумме углов ВСН и НСК. Известно, что угол НСК равен 15 градусам. Следовательно, угол ВСН=уголВСК-уголНСК= 45-15=30 градусов.
Так как угол ВНС прямой (СН высота треугольника АСВ), то по сумме углов треугольника СВН, угол СВН= 180-90-30=60 градусов.
Угол ВАС треугольника АВС в соответсвии с этим равен 180-90-60=30 градусов.
По свойству прямоугольного треугольника, в котором напротив угла, равного 30 градусов лежит катет, длина которого равна половине длины гипотенузы.
Следовательно, ВС=½АВ=6 см.
ответ: ВС=6 см
I в. с = 41 см; S = 180 см².
II в. в = 7 см; S = 84 см².
Объяснение:
Площадь прямоугольного треугольника равна половине произведения его катетов; S = ав/2.
Катеты или гипотенузу можно найти с теоремы Пифагора - В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. с² = а² + в². Из этого а² = с² - в² и в² = с² - а².