∠B = 30°
Пояснение:
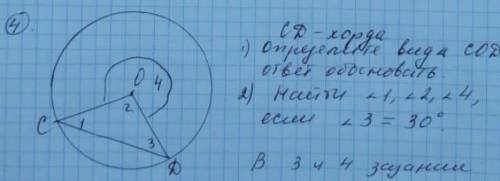
Дано: Δ АВС, ∠С = 90°, ∠АОС = 105°, биссектрисы CD и АЕ, что пересекаются в точке О
Найти: меньший острый угол Δ АВС
Решение
∠CAO = ∠OAD (так как биссетриса AE делит угол ∠А пополам)
∠ACD = ∠OCB= ∠C/2 = 90°/2 = 45° (так как биссетриса CD делит угол ∠C пополам)
Рассмотрим Δ CAO, в котором ∠CAO = 45°, ∠АОС = 105°, ∠CAO - ?
Так как сумма всех углов в треугольнике равна 180°, то
∠CAO = 180° - (105° + 45°) = 180° - 150° = 30°
∠CAO = ∠OAD = 30°, следовательно ∠А = ∠CAO + ∠OAD = 60°
Рассмотрим Δ АВС, в котором ∠С = 90°, ∠А= 60, ∠B - ?
Так как сумма углов при катетах в прямоугольном треугольнике равна 90°, то
∠B = 90° - ∠А = 90° - 60° = 30°
ответ: ∠B = 30°
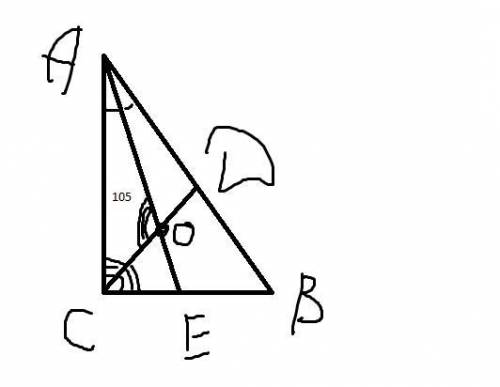
Объяснение: в треугольнике с 30,60,90 есть такое свойтво наименьший катет А(противолежит углу 30 ) а другой катет (протеволежит углу 60 )A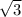
а гипотенуза равна 2A так вот в 4 задаче так и выходит СD=3,5 AD=7 и AC=3,5 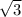тогда исходя из свойства угол D=60гр так как противолежит AC , так как СB=CD исходя из того что AC общая высота и для ACD и ABC то треугольник ABC равносторонний и угол В=60 5) тут аналогично используем тоже самое свойство уголs KPC=30 ; PKC=60 ;CKE=30;CEK=60 тогда СE=4,5 так как противолежит углу в 30гр и СK=4,5 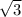; а PC=CK* = 
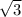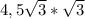=13,5 ответ CE=4,5 PC=13,5 если вам интересно откуда взялось это свойство то почитайте в интернете свойства треугольника с 30,60,90 градусами
по теореме круга угол 2=90
мы знаем что угол 3=30
1угол=180-2угол-3угол=180-90-30=60 г
4угол=2угол+4угол=360
4 угол=360-90=240г
ответ: 1угол-60, 2 угол-90, 4угол-240
Объяснение: